Suivez-nous sur X
|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement
|
|
David Brunet
|
|
|
|
En pratique : Volumm 4D - Arbres et volumes découpés
(Article écrit par Marcel Delord et extrait d'Ami-GrafX - février 1995)
|
|
Dans Ami-GrafX numéro 4,
j'ai traité la façon de découper une photo pour en faire un élément de décor plus utile qu'un
simple effet de texture. Dans ce nouvel exemple d'aujourd'hui, je montre comment il peut être
agréable de construire des arbres très réalistes sans utiliser des modèles mathématiques (genre fractals).
L'avantage de ce procédé est de construire sa maquette de façon traditionnelle et de pouvoir contrôler
sa création pratiquement au pixel près. La forme des feuilles, leurs couleurs, leurs dispositions ne
sont pas traduites par des données mais simplement dessinées. Pour l'artiste, cette méthode lui
permettra de conserver son style propre. Le photographe pourra utiliser ses photos. Les inconditionnels
de programmes scientifiques pourront quand même utiliser leurs fractales 2D.
Le lancer de rayon (plus connu sous le terme de "ray tracing") donne un rendu d'un réalisme bien connu. Plaquer des
textures sur des volumes peut parfois suffire pour simuler un grain de pierre ou des fibres de bois.
Il est plus difficile d'obtenir par cette méthode l'imitation des arbres car ce sont des volumes d'aspects
plus ou moins découpés. Des arbres représentés de la sorte paraissent pétrifiés car leurs contours ne
sont pas crédibles. Mais cela peut servir d'approche. Pour chaque espèce d'arbre, il est possible de
créer un modèle plein en partant de volumes simples (sphères, cônes, cylindres...). A ce stade
(image A), il n'est pas utile de compliquer la maquette car le résultat dépendra en grande partie de la
préparation des textures et de l'utilisation de la fonction "Opacity mapping" (placage d'opacité)
de Volumm 4D.
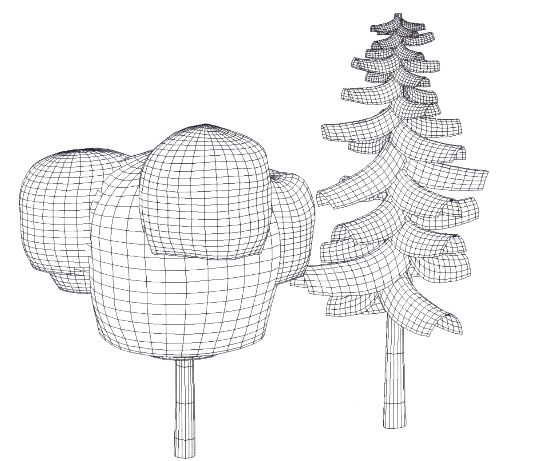Image A
L'image B représente la simulation du feuillage de l'arbre de gauche. C'est un travail réalisé avec
Designer de MicroGrafx en vectoriel puis exporté en bitmap. Ce logiciel mériterait un détour car
il est très puissant.
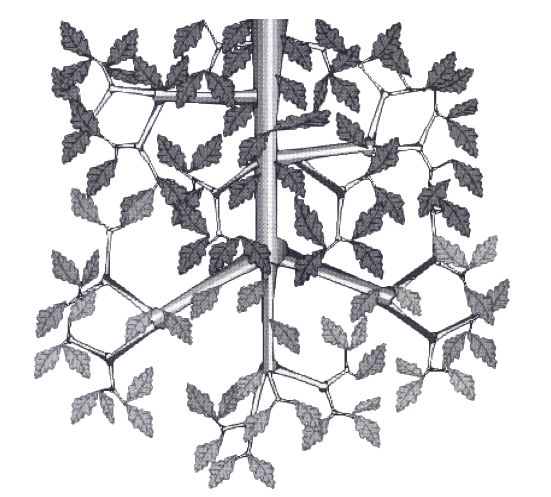Image B
L'image C a été réalisée avec Picture Publisher du même éditeur. Elle servira de cache pour
le placage d'opacité de Volumm 4D. Le processus est le même que pour celui traité dans le numéro 4
de cette revue.
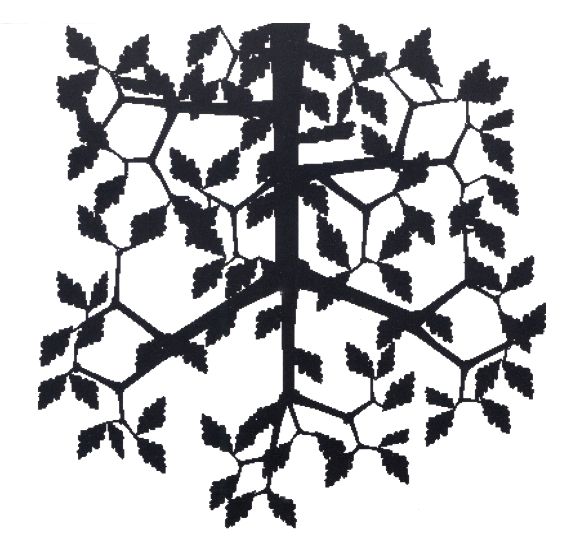Image C
Je ne vais donc pas m'attarder sur la technique. Il faut remarquer quand même une
particularité utile sur l'image B : le dessin de la branche qui se termine en haut et au centre
de l'image ainsi que les feuilles qui ne coupent jamais le bord de l'image. Prenons l'exemple
d'une sphère : son sommet (voir image A) sera le point de départ de la branche et les feuilles
irons vers le bas. Si je duplique le placage (seulement en horizontal), j'obtiens plusieurs branches
partant du même sommet de cette sphère. Il suffit de placer la sphère de manière à faire coïncider
son sommet avec une extrémité de branche plus grosse ou du tronc.
La relation avec le travail de dessin 2D (ou de photos) est ici très liée avec le modelage 3D. En changeant de modèle
et de dessin, il est très facile de créer autant d'arbres différents mais toujours très personnels.
L'image finale donne un aperçu des possibilités.
|
