|
Jeudi 19 juin 2025 - 08:54 |
| Translate |
|
| Rubriques |
| Réseaux sociaux |
|
| Liste des jeux Amiga |
|
| Trucs et astuces |
|
| Glossaire |
|
| Galeries |
|
| Téléchargement |
|
| Liens |
|
| Partenaires |
|
| A Propos |
|
| Contact |
|

|
|
Bonjour à tous. C'est de mouvements dont nous allons parler cette fois.
Le projet présenté nous vient d'un de nos lecteurs, il est assez important pour qu'il ne soit guère possible d'en faire le détail complet, même en deux articles. Je n'indiquerai donc pas les habituels paramètres relatifs aux ressources et aux temps de modélisation/calcul. Sachez simplement que vous pouvez modéliser ce qui va suivre avec les versions 3.0 et 3.2 d'Aladdin.
Le projet qui nous intéresse m'a été envoyé par Stéphane Cotantin. Stéphane est un passionné à la fois d'Aladdin et de mécanique. Son activité professionnelle l'amène à côtoyer quotidiennement différentes machines dont les mécanismes complexes lui ont fourni d'excellents supports pour ses recherches de modélisation. Ce sont les résultats de ces recherches que nous allons, avec sa permission, vous dévoiler ce mois-ci. Il s'agit du système came-levier. L'intérêt du projet réside dans le fait que Stéphane a réussi à relier logiquement le mouvement de la came (rotation) et celui du levier (translation ou rotation alternative uniformément variée liée au profil de la came). Personnellement, j'ai trouvé intéressant que, une fois n'étant pas coutume, on laisse un peu de côté les scènes spatiales ou domestiques, pour se pencher sur un peu sur les machineries.
Le projet de Stéphane Cotantin est donc d'une machine automatique d'imprimerie, où les pièces sont alimentées, marquées et finalement éjectées, tout cela à partir du seul mouvement de rotation d'un moteur (dont la fréquence de rotation est supposée constante). Nous allons dans cette rubrique "démonter" quelque peu la liaison cinématique entre le mouvement de rotation principal et celui du levier de marquage. La figure 1 nous permet de mieux comprendre le fonctionnement de la machine et des mouvements.

Figure 1
- Pour CM, il s'agit du mouvement oscillant permettant le marquage des pièces.
- Pour CAE, il s'agit d'un mouvement oscillant également transformé en translation alternative permettant, grâce à un piston, l'alimentation des pièces sur un drageoir.
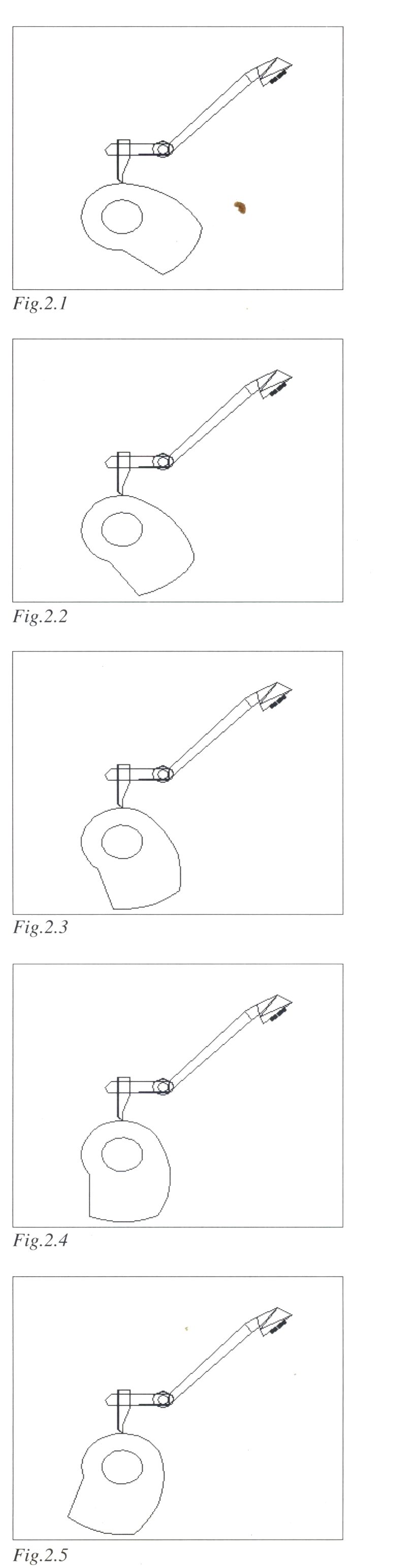
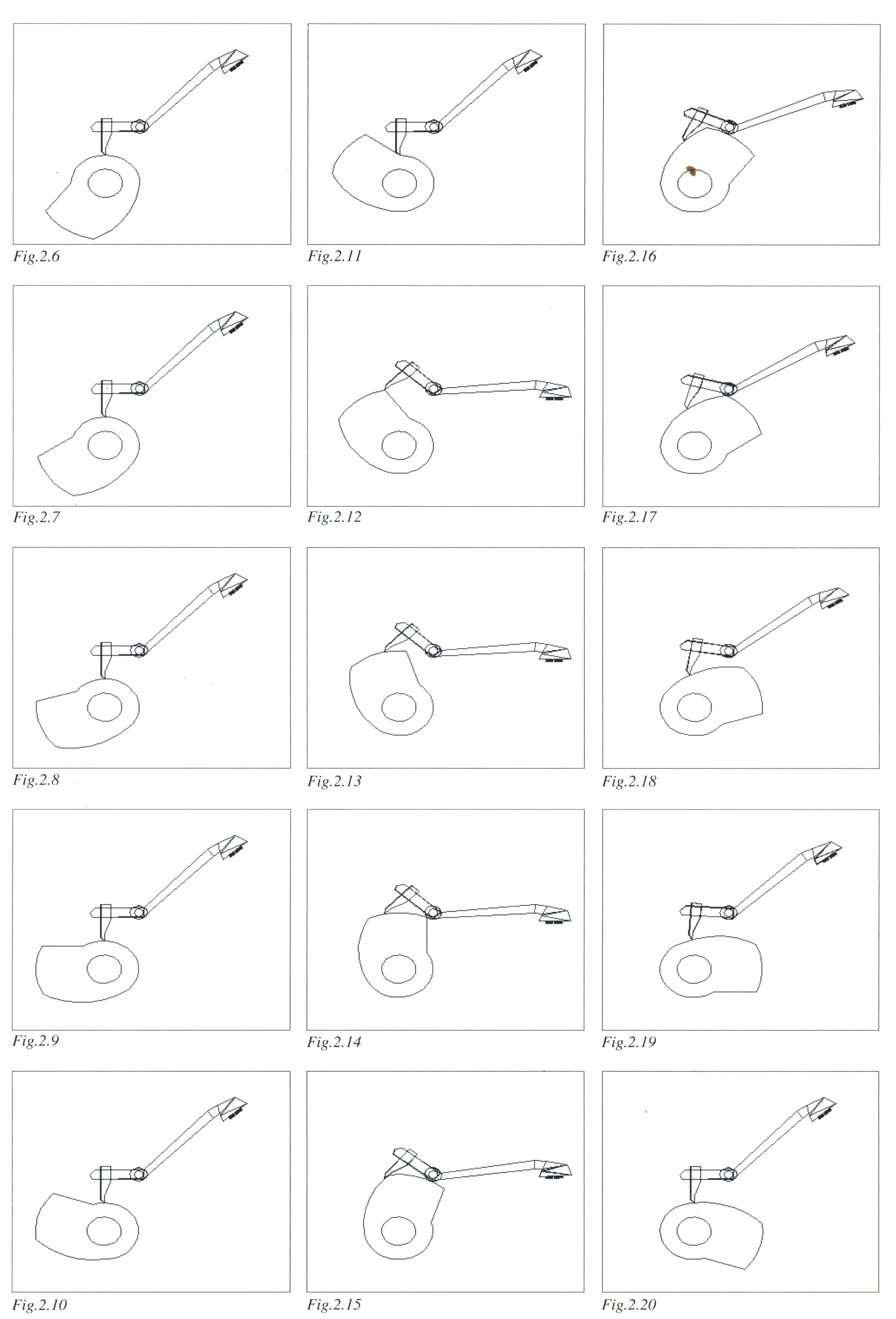
Voilà pour la description cinématique. Nous nous intéresserons principalement, comme nous l'avons dit, à la liaison came-levier pour le marquage. La figure 2 montre en 20 images la décomposition du mouvement obtenu. Nous reviendrons sur les différentes étapes de ce mouvement.
Came pour mouvement de translation
Avant de décortiquer le système modélisé par Stéphane Cotantin, nous allons, au travers d'un exemple plus simple, poser les bases du modelage du couple came-levier. Il s'agira d'un levier décrivant simplement un mouvement de translation alternatif suivant une direction verticale (piston de moteur à explosion, par exemple). La figure 3 représente un système came-levier type, on y observe que, s'il est facile de déterminer les points morts hauts et bas de la came (positions début et fin de course), le reste est moins évident, même pour un mouvement que l'on peut qualifier de simple.
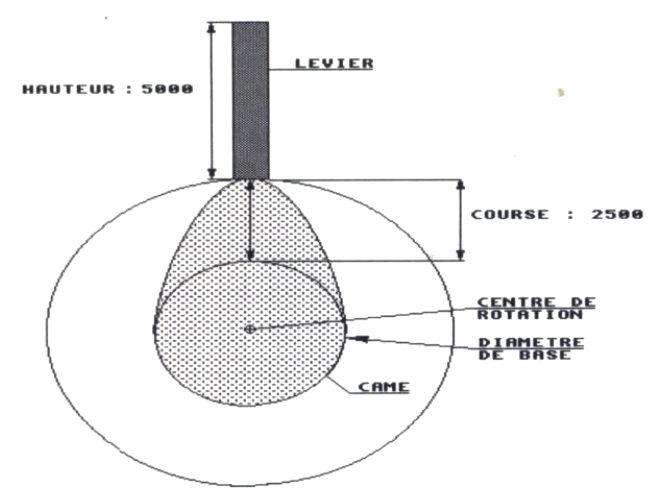
Figure 3
Le levier
Il sera constitué d'un rectangle de 5000 de haut et de 500 de large (unités du modeleur d'Aladdin). Passez en "Flat Y" (Plat Y) et ouvrez "Tools/Make Rectangle" (Outils/Faire Rectangle) avec X500, Y0 et Z5000.
Le chemin du levier
La course du levier (distance entre les points morts haut et bas, ou distance parcourue par le levier), sera de 2500. Nous créons un chemin partant du centre du rectangle (point facile à repérer, c'est aussi le centre du repère) de 2500 de long. Cliquez avec le bouton droit sur "Page Center" (Centrer page), cela a pour effet de ramener l'ATP sur l'origine. Dessinez le chemin à main levée en vous aidant du bord gauche de l'écran pour guider le pointeur et créez un segment de 2500 de long (Z-2500). Ouvrez "Make Poly a Path" (Faire du Palygone un chemin) et activez "Status" (Statut) de "Globals".
Activez également le bouton de contrôle "Spline" derrière "Start%" et chargez la spli-ne "Bounce at Half" (Rebond à la moitié). Activez "MirrorY" (MiroirY) pour retourner la spline, nous aurons ainsi un mouvement "croissant" par rapport au sens de chemin. Ensuite, cette spline présente des variations de pente entraînant des effets d'accélération au départ et à la fin, mais le changement de direction se fait sur un point de rebroussement, ce qui est impossible dans la pratique, dans la mesure où cela supposerait une accélération infinie. Nous allons donc placer les deux points de tension du centre de telle sorte que la tangente soit nulle, les coordonnées seront (0.3,100) et (0.7,100) respectivement. Nous aurons ainsi une vitesse décroissant jusqu'à 0 avant l'inversion de sens (figure 4).
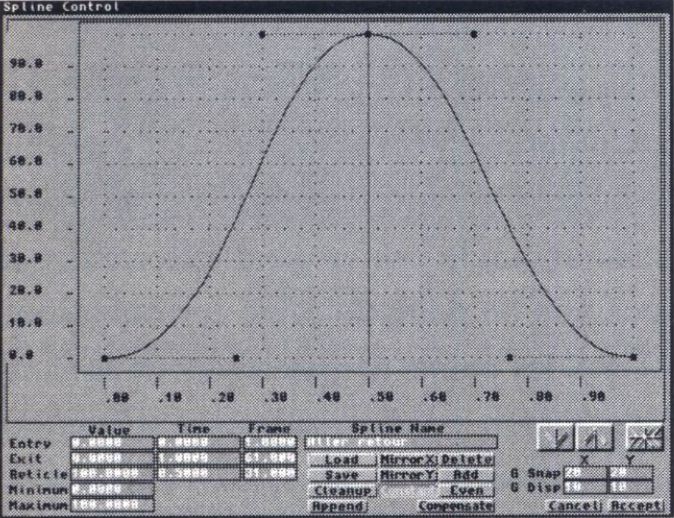
Figure 4
Pour terminer, donnez un nom à votre spline (j'ai choisi "Aller retour"), et sauvez-la, elle vous sera utile. La mise au point que nous venons de faire, et qui n'a d'autre but que de rendre le mouvement réaliste, a par contre compliqué le développé de la came correspondante. Heureusement, le modelage n'en sera pas plus difficile pour autant, comme nous allons le voir maintenant.
Sélectionnez le chemin et accédez à la fenêtre de contrôle spline. Entrez la valeur 20 pour "Grid Display en X" (Affichage de la grille en X), on aura ainsi 20 points en horizontal, de 0,05 en 0,05, et 40 pour "Grid Display en Y" (Affichage de la grille en Y), le pourcentage de déplacement est ainsi découpé en pas de 2,5, ce qui permettra une précision de lecture suffisante. Il s'agit de lire les valeurs de déplacement (en %) correspondant à chaque pas en X, donc à chaque moment particulier du cycle.
La spline étant symétrique par rapport au centre, nous ne relèverons que les dix premiers points. On utilisera les zooms et les flèches de directions pour déplacer la spline dans la fenêtre. La figure 5 donne les valeurs relevées.
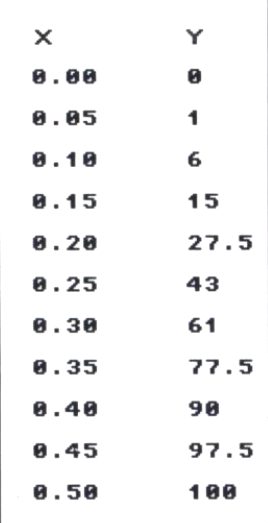
Figure 5
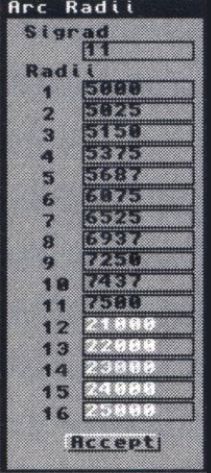
Figure 6
La came
Comme prévu, nous allons créer un arc, mais sur 180° seulement (nous n'avons prélevé que la moitié des points), et avec des rayons différents. Ouvrez "Tools/Make Arc" (Outils/Faire Arc) et entrez 180°, 10 segments (donc 11 rayons) et ouvrez "Set radii" (Régler radii) pour entrer les valeurs comme indiqué figure 6, spécifiez 11 dans "SigRad" et refermez puis acceptez. Vous obtenez la demi-came tant désirée.
Il ne reste plus qu'à la cloner et à faire un miroir par rapport à Y (mettez l'ATP sur le segment vertical de la came et choisissez ATP dans Miroir). Groupez les deux demi-cames, c'est terminé pour la forme.
Vous devez maintenant amener la came de telle sorte que son point supérieur soit tangent à la base du levier. Il suffira de repérer la position des deux points et de les faire coïncider. Sélectionnez le levier par un des points inférieurs, activez le mode d'entrée manuelle (F10) et relevez la coordonnée Z (cela doit être 2500). Sélectionnez ensuite la came par le point supérieur et dans le mode manuel, modifiez la valeur Z avec le nombre précédent (2500). Activez "Move Poly" (Déplacer Polygone) puis "Accept" (Accepter). La came est en bonne position.
Il faut maintenant dessiner le chemin de rotation en partant du centre de rotation de la came. Un rapide calcul nous montre qu'il se trouve en X0,Y0,Z7500. Ouvrez "Tools/Set ATP" (Outils/Réglage ATP) et entrez ces coordonnées. A partir de là, utilisez le mode main levée pour dessiner un petit triangle (comme je l'ai conseillé dans mon dernier article : chemin de rotation = triangle). Ce sera le chemin de rotation du cercle de base de la came et son point 0 en occupe le centre. Faites de ce triangle un chemin dans la fenêtre duquel on entrera simplement 360 pour "Rotation Y Exit".
Vous devez maintenant avoir quelque chose ressemblant à la figure 7. Pour plus de clarté, j'ai ajouté un cercle de 2500 de rayon sur le même centre pour le matérialiser. Vous pouvez faire de même, ou pas. Assignez la came à ce nouveau chemin et prévisualisez en 60 images.
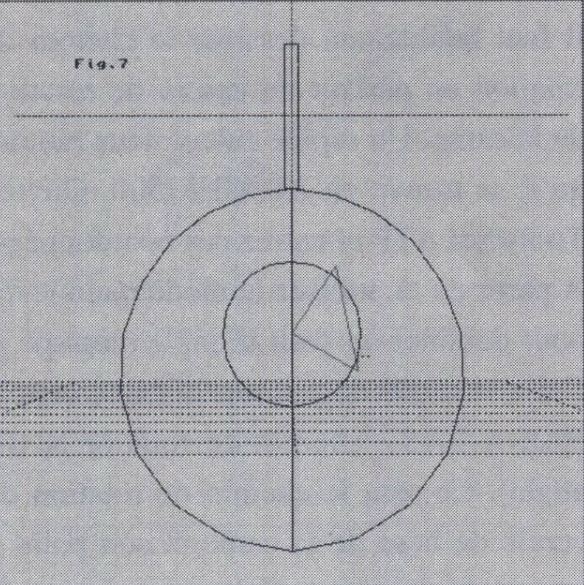
Figure 7
A noter aussi que la précision du profil de came est proportionnelle au nombre de points relevés sur la spline (il s'agit d'un échantillonnage). En utilisant ma méthode de modélisation par arc à rayon variable, vous serez limités à 32 points, puisque Aladdin ne vous laisse entrer que 16 rayons, dans le cas d'une came symétrique, et à 16 (là, c'est un peu juste) pour une came quelconque. Il sera, bien sûr, toujours possible de multiplier le nombre de point en limitant l'arc aux portions critiques de la came, puis de rendre, par rotation, les différentes portions contigües. Ainsi, on peut modeler la came en autant d'arcs que nécessaires.
Cela peut devenir fastidieux, mais c'est très précis. Il y a encore d'autres solutions pour modeler une came, et avant d'attaquer le problème des leviers en rotation, nous allons faire un rapide inventaire.
Dessiner une came
Je proposerai quatre méthodes principales, en plus de celle que je viens d'exposer, dont je préciserai à nouveau qu'elle est de loin la plus précise et la plus "logique", dans la mesure ou le mouvement du levier est une translation ; quelle que soit la méthode choisie, il est de toute façon indispensable de passer par un relevé de points sur la spline du mouvement. Tout part de là.
1. Dessin 2D puis conversion (tous logiciels 3D)
Le principe est simple : dans votre logiciel 2D, vous dessinez votre came en haute résolution et deux couleurs, puis vous la convertissez (Interchange, Vertex, Pixel Pro) en un polygone. Vous pourrez ensuite, grâce à l'un des trois logiciels précités, l'exporter dans le format de votre choix (.geo ASCII ou Draw4dPro pour Aladdin). Attention cependant aux effets d'escalier dus à la représentation en pixels du dessin 2D. Vous pouvez atténuer ces escaliers avec des fonctions de lissage, mais au risque de perdre des points significatifs.
2. Utiliser le "Mode Trace" (Aladdin seul)
Cette méthode est très utile lorsque vous ne disposez pas d'un convertisseur. Elle utilise le mode "Trace" d'Aladdin. Dans ce mode, Aladdin affiche en fond une image IFF directement dans le modeleur, ce qui vous permet de "tracer" à main levée votre polygone par-dessus, un peu comme un calque ; on l'utilise surtout pour ajuster précisément des polygones à des textures de forme spéciale, l'image IFF étant ensuite plaquée sur le polygone qu'elle a servi à créer. Dans notre cas, l'image IFF sera le dessin en 2D de la came, obtenue comme dans la méthode 1.
3. Travailler à partir de splines (Aladdin, Imagine, Freeform, tous logiciels 3D permettant de dessiner en mode spline)
Pas forcément simple, mais cela vous permet d'avoir des profils précis. Avec Aladdin, vous devrez transformer vos splines en polygones. Le mode d'entrée manuelle vous permettra de retoucher les profils en travaillant directement sur les coordonnées des points.
4. Modifier un cercle manuellement
Une came ressemble assez souvent à un cercle déformé, il peut parfois être intéressant de partir de cette forme et d'en retoucher certains points. Là encore, le mode d'entrée manuelle sera d'un précieux concours.
Came pour mouvement de rotation
Nous arrivons finalement au projet de Stéphane Cotantin. Le modelage est un peu plus complexe car, cette fois-ci, le levier n'est plus animé d'un mouvement de translation, mais de rotation ; de plus, le mouvement présente des paliers stationnaires. La spline (figure 8) nous permet de relever les images critiques traduisant les changements de "rythme".
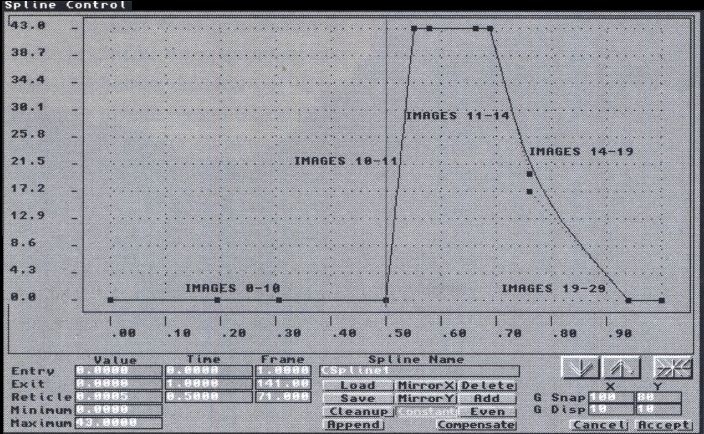
Figure 8
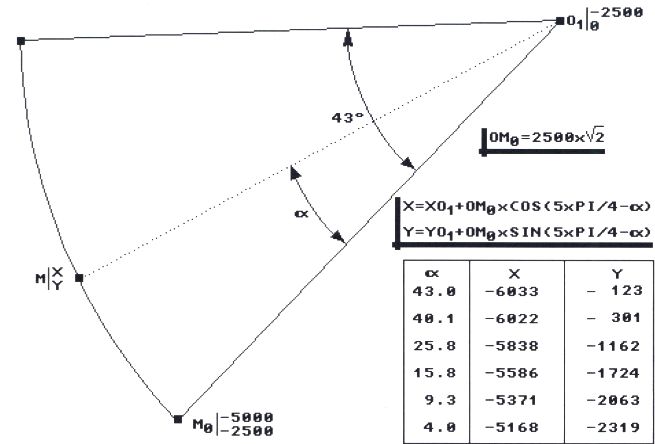
Figure 9
Ce sont ces points qui devront servir de guide pour le profil de la came. Dans le projet de Stéphane Cotantin, le rayon de base est de 5000. Stéphane Cotantin a utilisé la méthode 2 (dessin 2D puis mode "Trace") pour modeler la came. Évidemment, certaines retouches sont nécessaires, dans la mesure où nous n'avons prélevé que les points de variation.
Voici comment, suivant la manière dont s'effectuent les transitions, on recrée le profil de la came :
- Paliers stationnaires (images 0 à 10 par exemple). Ils se traduisent dans la spline par des segments
horizontaux. Il est important de connaître le rayon à l'entrée du palier. Ensuite, le rayon de came
reste constant jusqu'à la prochaine transition.
- Variations linéaires (images 10 à 11 par exemple). Ce sont les segments de droite inclinés de la spline.
Suivant la pente, et le nombre d'images concernées, on aura une droite (comme c'est le cas pour les deux
images 10 et 11) entre les deux rayons de la came. Le rayon augmentera ou diminuera suivant le sens du déplacement
et le signe de la pente. Si le nombre d'images est important, le rayon devra augmenter progressivement, et
un relevé de points intermédiaire sera nécessaire.
- Variations exponentielles (images 14 à 19 par exemple). Il faut échantillonner la spline, de telle sorte que la suite de segments obtenue soit aussi proche que possible de la courbe. Les segments successifs seront ensuite traités comme des variations linéaires.
- Splines non continues, elles supposent, dans le cas des mouvements, des accélérations infinies (bien sûr, si vous arrivez à les reproduire dans la réalité, pas mal de grandes sociétés et moi-même sommes preneurs !).
- Points de rebroussement (comme dans Bounce_at_Half.csp à mi-cycle), même motif que ci-dessus, et même punition.
- Changement de sens à vitesse non nulle, encore une fois, peu de mécanismes supportent ce genre de secousses.
Cela aussi représente un point important de l'authenticité du mouvement modélisé. Deux aspects sont à prendre en considération, l'aspect géométrique et l'aspect technologique.
Pour l'aspect géométrique, il faudra vérifier qu'il n'y a pas interférence entre la came et le levier (au besoin, retoucher le profil de came et/ou du levier). Normalement, chaque transition doit être précédée d'une phase de repos (sur 2 degrés) où le mouvement est stationnaire. Le rayon de base doit être suffisamment grand devant la course pour que la tangente au rayon de came soit le plus souvent possible perpendiculaire au levier en contact.
Pour l'aspect technologique, le contact entre la came et le levier donne naissance à des efforts importants. Ces efforts entraînent un frottement significatif, voir un arcbouttement (le levier se "plante" dans la came). L'extrémité du levier devra être le plus souvent demi-cylindrique. Le contact surfacique est ainsi transformé en contact linéaire, et la cylindricité engendre des angles de dégagement entre le levier et la came. On pourra également ajouter un galet en bout du levier, le frottement de roulement se substituant au frottement de glissement. Encore une fois, ces aménagements n'ont pour but que de se rapprocher du modèle réel.
Conclusion
S'il fallait conclure... Ce type de projet cinématique montre assez quelle souplesse et quelle puissance Aladdin peut offrir dans le domaine particulièrement riche des mouvements. Le système de contrôle spline se prête admirablement bien à la gestion des mouvements mécaniques (oscillation, translation alternative, rebond, etc.). Bien maîtrisé, le contrôle spline palliera souvent l'absence de gestion des collisions, frictions et autres frottements. Les inconditionnels regretteront cette absence, cela sera pour nous l'occasion de rappeler qu'Aladdin est résolument orienté vers la productivité (rapidité de modélisation et de rendu) : ceci découle de cela.
|