Suivez-nous sur X
|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement
|
|
David Brunet
|
|
|
|
En pratique : Tracer l'ensemble de Mandelbrot
(Article écrit par Peter B. Schroeder et extrait de Byte - décembre 1986)
|
|
Plus l'affichage est intéressant, plus il faut de temps pour le générer
Certaines personnes peuvent lire une partition de musique et, dans leur esprit, entendre la
musique rendue de manière plus glorieuse que par n'importe quel orchestre. D'autres peuvent
voir, dans leur esprit, la grande beauté et la structure de certaines fonctions mathématiques
et de certains systèmes numériques. Les personnes moins expérimentées, comme moi, ont besoin
d'entendre de la musique et de voir des nombres rendus pour apprécier leurs structures.
L'ensemble de Mandelbrot est l'une des structures mathématiques intrigantes que vous pouvez
explorer avec le Commodore Amiga. Dans The Fractal Geometry Of Nature (voir référence 1),
Benoit Mandelbrot définit une fractale comme "un ensemble pour lequel la dimension de Hausdorff
Besicovitch [dimension fractionnelle] dépasse strictement la dimension topologique".
Vous pouvez utiliser les fractales pour décrire les aspects fragmentaires de la nature. Les
fractales aléatoires peuvent simuler des paysages et des objets dans la nature, tels que des
arbres et des montagnes. Les modélisateurs mathématiques peuvent les utiliser pour simuler la
dégradation du littoral et ses effets sur la pêche. Les biochimistes peuvent utiliser les fractales
pour caractériser l'irrégularité des surfaces des protéines et son influence sur les interactions
moléculaires. Vous pouvez les utiliser pour modéliser le climat et prévoir d'autres événements
apparemment aléatoires et chaotiques (voir référence 2). Vous pouvez les utiliser pour découvrir
l'ordre là où l'on croyait qu'il n'y en avait pas. Même les processus de l'ontogenèse, c'est-à-dire
le développement d'un organisme individuel, qui se sont révélés insaisissables, pourraient être
explorés à l'aide de la géométrie fractale.
Pour commencer, vous devez connaître les définitions des nombres complexes, réels et imaginaires.
Un nombre complexe est un nombre de la forme a+bi, où "a" et "b" sont des nombres réels,
et i=√-1. Un nombre réel est un nombre dans lequel il n'y a pas de partie imaginaire,
et un nombre imaginaire est un nombre complexe dont "b" n'est pas égal à zéro ; certaines
définitions exigent également que a=0.
Les ingénieurs et autres personnes s'occupant de mathématiques vectorielles trouvent les
nombres imaginaires utiles. Par exemple, si le vecteur "b" peut être tourné de 180 degrés
pour pointer dans la direction opposée en le multipliant par -1, de sorte que "b" est égal
au vecteur "-b", et qu'il existe un nombre, "a", qui fait tourner le vecteur de 90 degrés,
alors a2 fera tourner le vecteur de 180 degrés et sera égal à -1 . Ainsi,
a=√-1.
Qu'est-ce que l'ensemble de Mandelbrot ?
L'ensemble de Mandelbrot est un ensemble de nombres z=c2+c où "c" est un nombre
complexe de la forme a+bi et où "z" élevé au carré de manière itérative ne produit jamais
une racine carrée de a2+b2 supérieure à 2. Notez que, puisque i2
est égal à -1, (a+bi)2 est égal à a2+2abi-b2, et que
l'élévation au carré itérative de ces nombres produit un résultat en dents de scie, non
différentiable. Si la somme des carrés dépasse 4 après un grand nombre d'itérations, elle
finira par approcher l'infini et, par définition, ne fera pas partie de l'ensemble de Mandelbrot.
Si l'on prend une matrice, "a" par "b", et que l'on élève itérativement au carré chaque
élément de cette matrice jusqu'à ce que la somme de leurs carrés dépasse 4 ou que l'on atteigne
1000 itérations, on peut déterminer un compte du nombre d'itérations que chaque élément du
tableau nécessite. Les éléments dont le nombre d'itérations est égal à 1000 font partie de
l'ensemble de Mandelbrot ; les éléments dont le nombre d'itérations est très élevé mais toujours
inférieur à 1000 sont proches de l'ensemble de Mandelbrot ; et ceux dont le nombre d'itérations
est faible en sont loin. Si vous attribuez des couleurs à chaque compte ou plage de comptes
et que vous coloriez chaque pixel de l'affichage matriciel en conséquence, vous pouvez représenter
graphiquement l'ensemble de Mandelbrot et ses nombres voisins. En un sens, les différentes
couleurs représentent la distance de la dimension fractale de l'ensemble de Mandelbrot pour des
éléments particuliers de la matrice.
Plus c'est petit, plus c'est grand
Les nombres fractals ont de drôles de qualités. Si vous agrandissez des zones proches de
l'ensemble de Mandelbrot, vous trouverez de minuscules répliques imparfaites de l'ensemble
de Mandelbrot plus grand. Si vous augmentez encore le grossissement, vous trouvez encore
plus de répliques minuscules associées, et ainsi de suite à l'infini. Ces composants sont
d'une grande beauté et présentent des structures exotiques, toutes différentes mais toujours
partiellement répliquées à un niveau plus petit.
Le grossissement que vous pouvez atteindre n'est limité que par la précision de votre ordinateur.
En C, l'Amiga stocke les nombres à virgule flottante en double précision sur 64 bits avec une
précision, par conséquent, d'environ 263. Il effectue tous ses calculs en virgule
flottante double précision, et sa plage pour les entiers longs est de -2 147 483 648
à 2 147 483 647 et pour les nombres en virgule flottante double précision de ±10,0-307
à ±10,0308 avec 15 à 16 chiffres décimaux de précision. Cette précision permet
d'examiner l'ensemble de Mandelbrot de manière plus détaillée qu'un microscope électronique ne
peut examiner la matière. Un microscope électronique peut produire une photo d'un objet agrandi
environ 1 000 000 fois. Il faut un grossissement de 300 000 à 400 000 fois
pour résoudre les facettes de la surface du virus de la poliomyélite. Si l'Amiga était un
microscope, son grossissement vous permettrait d'examiner les atomes qui composent ces facettes.
Les zones dignes d'intérêt sont celles qui sont étroitement associées au grand ensemble de
Mandelbrot de la photo 1, qui représente les nombres de -2,0 à 0,5 sur l'axe des x et de
-1,25 à 1,25 sur l'axe des y. Son étendue est donc de 2,5 sur les deux axes.
Photo 1 : une instance de l'ensemble de Mandelbrot représentant les nombres de -2,0 à 0,5
sur l'axe des x et de -1,25 à 1,25 sur l'axe des y.
Les photos 2 et 3 sont des agrandissements successifs de la petite zone délimitée de la photo 1,
chacune ayant une portée égale à 1/20 de celle de la photo précédente. La zone rectangulaire
délimitée sur toutes les photos montre la zone agrandie sur la photo suivante.
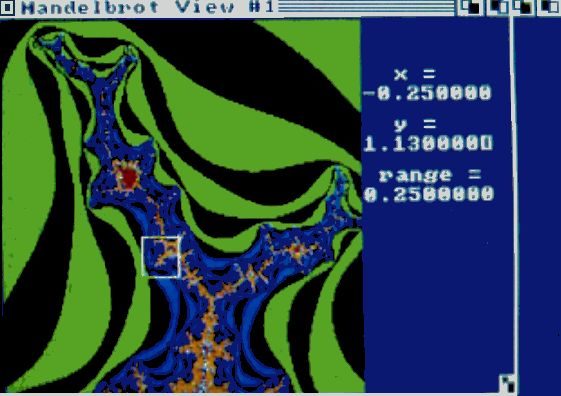Photo 2 : agrandissement du détail de la petite case de la photo.
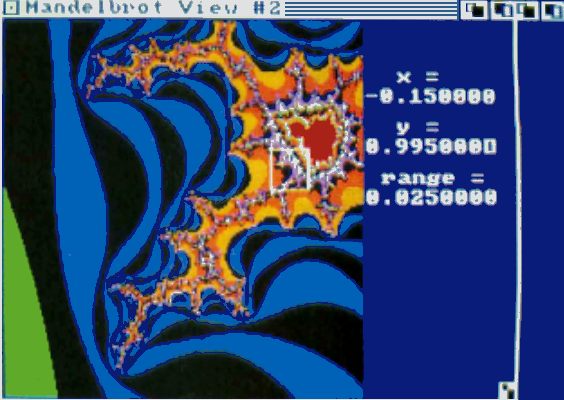Photo 3 : agrandissement du détail de la petite case de la photo 2.
Les programmes
A. K. Dewdney a fourni l'algorithme permettant de décrire graphiquement l'ensemble de Mandelbrot
dans Scientific American (voir référence 3). Mes programmes mettant en oeuvre cet algorithme
sont écrits en Lattice C ; ils ont produit les photos 1 à 3. Bien qu'ils prennent un certain
temps à s'exécuter, ils semblent rapides par rapport à une implémentation BASIC que j'ai
d'abord essayée.
DOSET.C (listing 1) vous permet de choisir les axes x,y où vous voulez commencer l'affichage
et de fournir la distance que vous voulez couvrir. Plus cette distance est petite, plus le
grossissement est important. Ces programmes peuvent prendre beaucoup de temps - des heures, voire
des jours - pour générer un affichage. Plus vous êtes proche de l'ensemble de Mandelbrot, plus
cela prend du temps.
Listing 1 : DOSET.C qui calcul l'ensemble de Mandelbrot. Vous aurez besoin de la
translator.library, de l'intuition.library, de la graphics.library et du narrator.device, ainsi que
du compilateur Lattice C pour exécuter ces programmes.
Vous devriez choisir un axe x,y près du bord de l'ensemble de Mandelbrot (coloré en rouge sur
les photos) pour une exploration plus approfondie. Si vous choisissez un point totalement à
l'intérieur de l'ensemble, l'affichage semblera prendre une éternité - pas littéralement, puisque
les programmes arrêtent de compter après 1000 itérations à chaque pixel - et l'affichage sera
d'une couleur unie. Si vous choisissez un endroit où chaque pixel prend les 1000 itérations
complètes (c'est-à-dire à l'intérieur du jeu proprement dit) et que vous générez un affichage
de 200x200 pixels, l'Amiga doit effectuer 40 millions d'itérations. Si une itération effectue
environ 20 opérations en virgule flottante en double précision, cela fait 800 millions d'opérations
en double précision (64 bits). Et si chaque opération nécessite la manipulation de tous les bits,
cela représente 51 milliards d'opérations sur les bits. En revanche, si vous commencez loin de
l'ensemble de Mandelbrot, vous finirez beaucoup plus vite, mais vous vous retrouverez avec un
affichage inintéressant. Choisissez donc un affichage qui inclut une zone à côté de l'ensemble
proprement dit, et peut-être même un peu de celui-ci.
VIEWSET.C crée un affichage graphique de 200x200 pixels à partir du fichier de données créé
par DOSET.C. Si vous voulez aller plus loin, essayez de modifier la séparation des couleurs
dans le programme. Avec la bonne séparation des couleurs, vous pouvez trouver toutes sortes
d'objets intéressants : des arbres, des oiseaux, peut-être même un autoportrait ou des millions
d'entre eux. Comme l'Amiga peut afficher jusqu'à 640x400 pixels, vous pouvez également créer
des affichages à haute résolution. Cependant, ces affichages prennent encore plus de temps à
générer.
Nouveaux horizons
Si vous vous intéressez à l'ensemble de Mandelbrot, bonne exploration. La progression est peut-être
lente, mais la région est immense et restera toujours largement inexplorée. En raison du temps
que cela implique, si vous souhaitez simplement regarder les affichages que j'ai déjà générés,
je vous enverrai une disquette pleine à mes frais (10 $). Vous pouvez la partager comme vous
le souhaitez.
Références
- Mandelbrot, Benoit B. "The Fractal Geometry of Nature". New York : W. H. Freeman and Company, 1983.
- Nicolis, C, et G. Nicolis. "Is There a Climatic Attractor? Nature, octobre 1984. pages 529-532.
- Dewdney, A. K. "Computer Recreations: A Computer Microscope Zooms in For a Look at the Most Complex Object in Mathematics".
Scientific American. Août 1985. pages 16-24.
L'auteur de cet article
Peter B. Schroeder est président de Biosystems Research Inc (11 550 Southwest 108 Court,
Miami, FL 33176). Il est un consultant biologique spécialisé dans les zones humides et
les estuaires. Il est titulaire d'un doctorat en biologie de l'Université de Miami à Coral Gables.
|
