 |
Mardi 27 janvier 2026 - 09:47 |
| Translate |
|
| Rubriques |
| Réseaux sociaux |
|
| Liste des jeux Amiga |
|
| Trucs et astuces |
|
| Glossaire |
|
| Galeries |
|
| Téléchargement |
|
| Liens |
|
| Partenaires |
|
| A Propos |
|
| Contact |
|

|
|
Les mathématiques sont considérées par beaucoup comme rébarbatives. Lorsque l'on voit la manière de les enseigner, surtout chez nous, on ne peut que leur donner raison. Notre approche classique des mathématiques consiste, à partir de concepts les plus immatériels et les plus généraux possibles, à développer des conséquences et des généralisations, sans souci aucun (bien au contraire, ce serait polluer le raisonnement) de raccorder ceci à une réalité physique quelconque. Plus c'est abstrait, mieux cela vaut. Heureusement, on en revient un peu.
Ceux qui survivent à ce traitement peuvent devenir mathématiciens, les autres décrochent très vite, et outre le fait que le manque de tout bagage mathématique peut causer certains problèmes pratiques, ils passent à côté de choses bien intéressantes, entre autres des aspects esthétiques des mathématiques quelque peu inattendus.
Les Anglo-Saxons (et en France assez souvent les physiciens) ont une approche didactique différente, partant volontiers de notions physiques et observables par tous, pour aller ensuite vers des concepts mathématiques qui, à l'arrivée, n'en sont pas moins tout aussi rigoureux que les nôtres. En particulier, ils font plus volontiers appel à des visualisations et à des simulations que nous.
Au demeurant, l'évolution de la pédagogie moderne donne de plus en plus de place à ces techniques comme moyen de découverte et d'ancrage de la connaissance. Les Américains utilisent volontiers les ordinateurs et calculateurs pour faire des mathématiques expérimentales, c'est ce qui a conduit Benoît Mandelbrot à faire découvrir les fractales qui portent son nom, les concepts mathématiques qu'elles recouvrent ayant en fait été étudiés par les Français Julia et Fatou au début de ce siècle.
C'est dans cet esprit d'approche expérimentale et amusante des mathématiques, que Doug Houck a conçu il y a quelques années un programme qui s'appelait Doug's Math Aquarium, lequel a évolué vers un outil splendide qui s'appelle MathVision, que je me propose de vous présenter.
Présentation
MathVision est un programme destiné à créer des représentations visuelles de fonctions mathématiques, des plus simples aux plus complexes, à des fins exploratoires, didactiques ou esthétiques ; ceci à l'aide d'une interface utilisateur complète, d'un compilateur de fonctions puissant, et de capacités graphiques très larges. Il peut également travailler par lots grâce à une interface ARexx bien conçue.
Tout d'abord, le classique déballage. D'une boîte ornée d'images qui vous mettent l'eau à la bouche, sortent trois disquettes et un manuel d'une bonne centaine de pages. Le programme vient en deux versions, une appelée MathVision.ffp qui utilise la bibliothèque mathématique Motorola en virgule flottante, et une version MathVision.ieee qui utilise la bibliothèque IEEE et fait appel, pour certaines routines, au coprocesseur s'il y en a un. La première version est en général plus rapide et calcule sur 7 chiffres significatifs ; l'autre peut calculer sur 16 chiffres, ce qui permettra, comme nous le verrons, des zooms assez profonds sur certaines fractales.
Les heureux propriétaires d'un disque dur installeront les deux versions car, selon ce que l'on fait, l'une ou l'autre est plus avantageuse. MathVision demande une machine munie d'au moins un Mo de mémoire ; sur une machine de 500 ko, on peut faire tourner son prédécesseur Doug's Math Aquarium avec lequel on peut déjà faire pas mal de choses.
La troisième disquette comporte des fichiers auxiliaires et des exemples, dont certains, peu documentés par ailleurs, sont d'un hermétisme profond, d'autres d'une grande simplicité, se prêtant volontiers à des manipulations expérimentales qui donnent des effets esthétiques intéressants.
MathVision peut bien sûr s'utiliser à partir d'une des deux premières disquettes. L'installation sur disque dur se fait sans aucun problème, elle n'est même pas documentée dans le manuel ! Il suffit de cliquer sur une icône, répondre à quelques questions, c'est net, propre et sans bavure, et ça marche.
Première approche
Une question se pose d'emblée : pourquoi encore un programme de visualisation de fonctions mathématiques, alors qu'il y en a déjà un bon nombre disponibles dans le domaine public et qu'au moyen d'un langage d'accès facile comme AMOS, on peut visualiser sans grande difficulté des fonctions mathématiques et faire de très jolis dessins ? J'espère que la réponse deviendra de plus en plus évidente au fur et à mesure de notre progression dans MathVision.
Le manuel vous met tout de suite dans l'ambiance en vous disant que faire si vous ne savez pas quoi faire de MathVision (sic), si vous ne connaissez ni l'algèbre ni la géométrie, si vous ne savez pas ce que c'est qu'une fonction, si vous voulez faire des animations grâce à l'interface ARexx.
En fait, je répète qu'il est parfaitement possible de se servir de MathVision sans connaître grand-chose en maths ; on peut charger des images toutes faites avec leurs formules, et s'amuser à modifier les paramètres et à observer les résultats. L'image en couleurs "Fresnel" a été obtenue moyennant une modification minime "au pif", d'un des nombreux exemples fournis sur les disquettes.
En fait, il vaut mieux quelques bases de maths tout de même ! Lançons MathVision et voyons comment se présente l'écran de commande. En haut, à gauche, les valeurs Xmin, Xmax, Ymin, Ymax correspondent au domaine que va balayer MathVision.
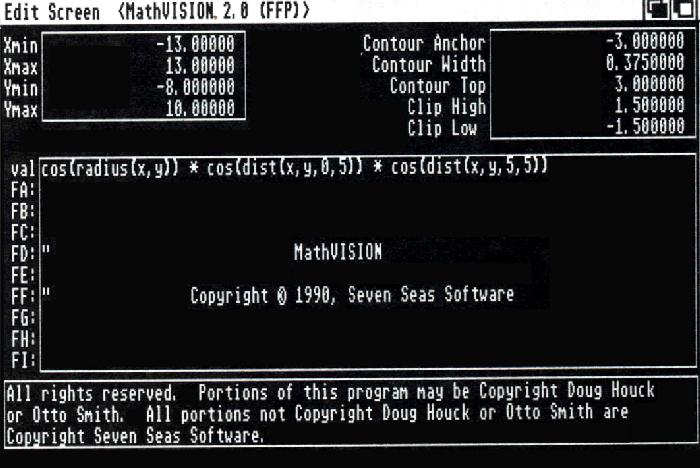
Figure 1
Les fonctions disponibles pour l'écriture des formules, sont représentées à la figure 2 qui montre l'écran d'aide. En positionnant le curseur sur le sigle d'une fonction, sa définition et un exemple de syntaxe apparaissent dans le bas de l'écran. On peut constater qu'elles sont d'une variété et d'un nombre impressionnants.
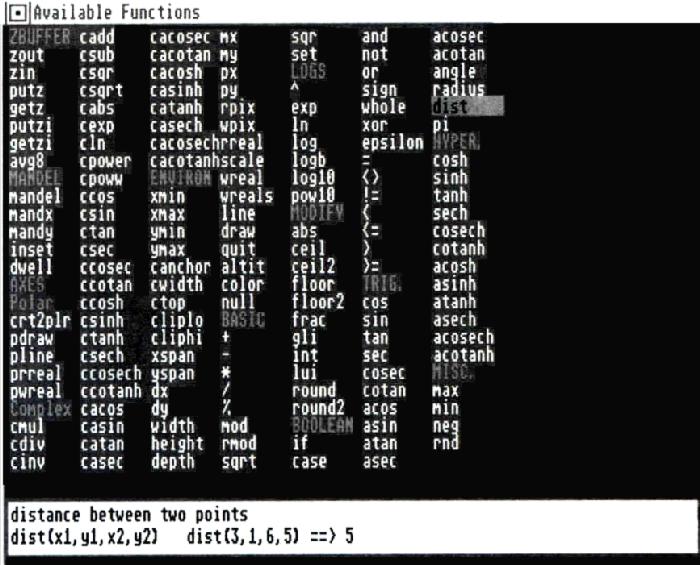
Figure 2
Simple qui correspond à une fonction d'une seule variable y=f(x) ; il tracera une courbe ou une famille de courbes sur son écran d'affichage.
Contour qui représente une fonction z=f(x,y) sous forme de lignes de niveau de couleurs différentes.
Perspective qui représentera la fonction sous la forme "filaire" bien connue des modeleurs 3D, soit sous la forme d'une surface colorée soit en damiers, soit en tranches dont les couleurs représentent les altitudes.
En haut et à droite, nous trouvons un cadre dans lequel s'affichent des valeurs correspondant à :
Contour Anchor, "ancrage du contour", définit la ligne de niveau la plus basse que nous souhaitons voir afficher.
Contour Width définit la gamme de valeurs de Z qui correspondra à l'utilisation d'une couleur de la palette.
Contour Top définit la ligne de niveau la plus haute à afficher.
Clip High et Clip Low définissent les mêmes valeurs pour le mode perspective.
On peut définir soi-même ces valeurs, ou laisser au programme le soin de proposer des valeurs qui donneront une image utilisable, à condition bien entendu que la définition de la fonction Z donnée dans le cadre central vaille quelque chose !
Enfin, la zone du bas est destinée à recevoir un commentaire. En résumé, on décrit une fonction, on donne un intervalle pour la ou les variables, et on affiche soit la courbe pour une fonction d'une variable, soit une série de contours (lignes de niveau), soit une surface en perspective pour une fonction de deux variables, le tout en définissant l'utilisation des couleurs pour l'affichage.
La figure 3 donne un exemple simple, il s'agit de la fonction :
| z = x*sin(y) + y*sin(x) |
...dans la région :
| (-10,10,-10,10) |
...dessinée en mode "Contour" avec le mode "Perspective" (opion filaire) en surimpression.

Figure 3
Dans le mode "Perspective", la touche "Tab" enclenche un cyclage des couleurs, le mouvement se faisant dans le sens de l'écoulement des eaux sur la surface, ce qui permet de localiser les bosses et les creux. Tout l'intérêt de MathVision se trouve dans le nombre immense de possibilités de jouer sur tous ces paramètres, dans la puissance du compilateur de fonctions qui gère ce qui est écrit dans la zone centrale et dans les modalités de traitement des résultats par une utilisation sophistiquée de la palette des couleurs. Il n'est pas possible de décrire dans un article de quelques pages toutes les possibilités offertes par les différents menus.
Il n'y a pas beaucoup de limites à ce que l'on peut faire, en se rappelant bien qu'il s'agit de représenter des fonctions de la forme : Z=f(x,y) univoques, c'est-à-dire pour lesquelles à chaque couple (x,y), ne correspond qu'une valeur de Z. Autrement dit, ne vous attendez pas à pouvoir représenter une sphère en trois dimensions. Ce n'est pas un programme de lancer de rayons !
Le compilateur de fonctions
Dans le rectangle central de l'écran de contrôle, nous avions noté la présence de lignes libres intitulées Val, FA, FB, etc. jusque FI. Dans la ligne Val est évalué le nombre "z" qui va définir une altitude, et donc, en mode "Contour", la couleur du pixel tracé et en mode "Perspective", la hauteur et la couleur du point affiché.
Comme nous le savons déjà, MathVision va parcourir l'écran, ligne par ligne, en faisant correspondre à chaque pixel des valeurs x et y qui dépendent des valeurs Xmin, Xmax, Ymin, Ymax que nous avons imposées.
Un cas simple
Mettons dans "Val" l'expression sqrt (x^2+y^2). Nous obtenons des ellipses concentriques. Pourquoi pas des cercles ? Parce que notre écran fait 640x512 pixels, il n'a donc pas un rapport hauteur-largeur (aspect ratio) de 1. Pour obtenir des cercles, nous donnerons comme limites pour "x" de -1,25 à 1,25 et le tour est joué.

Figure 4
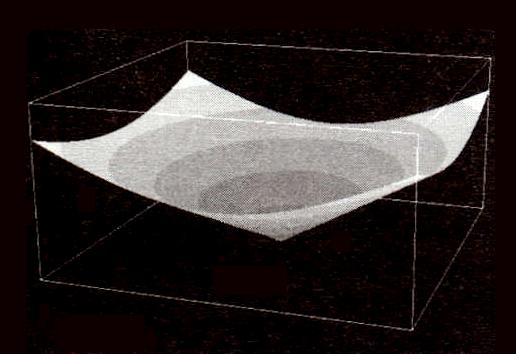
Figure 5
Sur un plan d'eau faisant ? 20x20 m, jetons un gros caillou, et laissons tomber en un autre point un galet plus petit. Pour cela, nous écrivons dans "Val" :
| 1,5*cos(dist(x,y,-10,3)+cos(5*dist(x,y,12,-15) |
Nous créons ainsi une onde sinusoïdale d'amplitude 1,5, centrée en -10, 3 et une autre onde sinusoïdale d'amplitude 1, mais de période 5 fois plus courte que la première, centrée en 12, -15. La figure en plan montre bien les ondes concentriques et leur schéma d'interférence.

Figure 6
|
Val fa + fd FA if(fi<18,0,fb) FB if(fi<30,fc,0) FC 1,5*sin(2*fi)*(fi-18)/12 FD if(fh<10,0,fe) FE if(fh<24,ff,0) FF sin(3*fh)*(fh-10)/14 FG FH dist(x,y,12,-l5) FI dist(x,y,-10,3) |
Le choix des valeurs des paramètres s'est fait par tâtonnements, pour obtenir une image parlante. En "Val", nous demandons l'addition des deux ondes :
- En FA et FB, nous forçons le résultat à 0 à l'extérieur d'une bande comprise entre les rayons 18 et 30, pour la première onde.
- En FC, nous décrivons l'oscillation, avec une amplitude qui croît linéairement entre des deux rayons (petite simplification malhonnête mais suffisante dans notre cas).
- En FI nous calculons la distance entre le point courant et le centre de l'onde.

Figure 7
Il y a des fonctions mathématiques d'expression relativement simple qui donnent de très jolies images. Voyez les images en couleur "Miroir de Cantor" et "Fresnel".

Figure 7b
Le compilateur de fonctions exécute ses lignes de haut en bas, sauf lorsqu'une ligne comporte un appel à une autre, comme c'était le cas dans notre dernier exemple. Normalement, le résultat de nos calculs sort en "Val", c'est cette valeur que prend MathVision pour colorer ses pixels.
Mais on peut procéder autrement. On peut écrire des fonctions Null(...) qui ne retournent aucune valeur, mais qui peuvent contenir des instructions particulières, comme écrire un pixel d'une couleur donnée à un endroit donné de l'écran, ou lire le numéro de la couleur d'un pixel et s'en servir dans un calcul. Ceci permettra par exemple de faire des anamorphoses.
Un cas d'utilisation de ces fonctions "Null" consiste à utiliser la fonction "Stipple" du menu "Contour", qui annule le balayage automatique de tout l'écran. En promenant la souris sur l'écran, les coordonnées du point courant sont lues, un calcul est fait et éventuellement un tracé, qui dépendra par conséquent du point où l'on se trouve.
L'exemple suivant illustre cette possibilité : sur le segment compris entre deux positions successives du pointeur, on trace un triangle dont le troisième sommet est situé dans la direction opposée à celle du centre de l'écran, ce sommet étant lui-même d'autant plus éloigné que les points de départ sont eux-mêmes éloignés du centre.
Je vous fais grâce du détail des formules, la figure 8 donne un dessin effectué par cette méthode.

Figure 8
Il n'y a pas beaucoup de limites à ce qu'on peut faire avec ces outils-là. De plus, on peut jouer sur la trame que composent les pixels pour obtenir d'intéressants effets de moirage.
Récursivité
Une caractéristique intéressante de l'ordinateur est la faculté de faire des calculs par itération. Si je veux par exemple calculer la septième puissance d'un nombre "x", je puis utiliser une méthode "analytique" :
|
input x print exp(7*log(x)) |
La technique itérative consiste à écrire :
|
input x P=1 for i=1 to 7 P=P*x next print P |
A noter que pour calculer une factorielle par exemple, il n'y a pas de méthode analytique, il faut procéder par itérations.
La technique récursive MathVision est :
|
Val fa(x,10) FA if(a2>=1,a1*fa(a1,a2-1),1) |
Ceci demande un petit mot d'explication sur les notations de MathVision. Lorsque dans une ligne Val, FA, FB, etc. on définit une fonction de plusieurs arguments, leurs valeurs sont stockées dans des variables dénommées a1, a2, a3, etc. et c'est sous ce nom qu'on rappelle ces arguments dans les autres lignes.
La technique employée ici est dite récursive car on voit que la fonction "fa" s'appelle elle-même.
Au commencement, le compilateur voit qu'on le renvoie à la ligne 2, pour calculer une fonction "fa" de deux arguments, "x" et "10". On veut dans le cas de l'exemple calculer 10 ! A la deuxième ligne, la fonction "fa" consiste à vérifier que le paramètre "a2", qui joue ici le rôle de compteur d'itérations, est plus grand que 1. Si c'est la cas, "fa" prend la valeur suivante : a1, c'est-à-dire "x", est multiplié par la fonction "fa" elle-même, qui a maintenant pour arguments "x" et le compteur "a2" décrémenté d'une unité.
Si le compteur a atteint la valeur 1, la condition de la deuxième ligne n'est plus vraie et l'itération s'arrête. Il n'y a plus qu'à remonter la pile en effectuant les multiplications, et à renvoyer la valeur à "Val".
Dans le cas particulier de l'élévation à une puissance, ce n'est certes pas la manière la plus simple de procéder ! Par contre, si nous prenons un cas d'itération un peu plus complexe, par exemple la fractale de Mandelbrot, l'avantage de cette approche devient plus évident. On écrira :
|
Val fa(x,y,fh) FA if(a3,fb(a1*a1,a2*a2,a1*a3,a3-1),0) FB if(a1+a2<4,fa(a1a2+x,2*a3+y,a4),a4) FH 50 |
Si ceci ne vous semble pas évident, c'est normal ; si comme moi vous n'y pigez rien au départ, mais avez l'envie de comprendre, l'acquisition de MathVision vous fera faire des progrès considérables dans la compréhension des mécanismes récursifs, probablement au prix de quelques maux de tête. Mais ce n'est pas tout... Comme si ce n'était pas assez, il y a encore les "hooks".
Les hooks
Hook (crochet, crosse, hameçon) est un terme volontiers employé par les informaticiens américains pour désigner un truc qui s'attache à un programme et en augmente les possibilités. MathVision vient avec une palanquée de ces accessoires, nous allons les regarder avec un détail variable, car le niveau de documentation de ces accessoires est variable, entre un minimum vital et presque rien. Ils n'en sont pas moins très intéressants et augmentent largement les possibilités de MathVision.
Ce sont des programmes que l'on lance comme tâches, et qui restent résidents tant qu'on ne les enlève pas, ou tant qu'on ne sort pas de MathVision. Lapalisse n'aurait pas mieux dit, mais le fait que MathVision sorte proprement en nettoyant correctement derrière lui mérite d'être signalé. Il y a des gens qui programment plus proprement que d'autres.
Les hooks se divisent en rien moins que cinq catégories :
- Gestion des couleurs.
- Algèbre complexe.
- Méthodes particulières d'affichage.
- Mémoire tampon.
- Divers.
MapColors : fait apparaître un écran secondaire qui reprend les couleurs de la palette. Pour chaque couleur, on peut définir la gamme de valeurs de la fonction qu'on souhaite lui faire correspondre, indépendamment des valeurs affichées dans le rectangle supérieur droit de l'écran. Ceci permettrait par exemple de faire apparaître une ligne de niveau particulière dans une couleur donnée.
HAM et HAM 256 : je n'ai tiré aucune image vraiment intéressante de ces modes HAM ; de plus, comme de bien entendu, lorsque des ruses de sioux ne sont pas prises, le HAM "dégouline". A mon humble avis, l'auteur aurait aussi bien fait de ne pas les inclure. Ces deux "hooks" sont un des rares points faibles de MathVision.
Hooks : Complex
Il y en a deux, Polar et Complex. Le premier permet de calculer en coordonnées polaires, ce qui est fort utile pour le calcul de figures de révolution. Il comporte une fonction de conversion de coordonnées cartésiennes en coordonnées polaires, et quatre autres fonctions pour lire les coordonnées polaires d'un point et tracer des droites entre des points définis par leur coordonnées polaires.
Comme son nom l'indique, l'accessoire "Complex" comporte non moins de 36 fonctions pour réaliser directement les opérations sur les nombres complexes. Ceci sera particulièrement intéressant pour réaliser des itérations à des puissances supérieures à 2. On s'ouvre ainsi la porte à des investigations sur des fonctions les plus délirantes, en particulier sur les Mandelbrot cubiques.
Hooks : méthodes particulières d'affichage
Focus et FocusDots : ces deux accessoires ont trait à des modes de présentation. "Focus" met d'office le "Sample Delta" à sa valeur la plus grossière, fait un tracé puis recommence avec des "Sample Deltas" de plus en plus fins, faisant apparaître progressivement l'image dans son détail.
A mon avis, on obtiendra de meilleurs effets par une programmation des images successives via ARexx, puis la création d'une animation par un programme du type AnimBuild ou Showiz, ou encore Deluxe Paint IV.
FocusDots : fait apparaître l'image en dessinant un pixel sur 8, une ligne sur 8, puis en remplissant progressivement. Même commentaire.
Parametric : c'est celui qui permet de sortir du mode d'affichage par balayage systématique de l'écran. Nous nous en sommes servis pour tracer l'image de la figure 8, et par ailleurs pour visualiser les orbites d'itérations de nombres complexes.
Hooks : mémoire tampon
Ça, c'est très intéressant. En première ligne du compilateur de fonctions, en face de "Val", on écrit : Zout(fa). Le résultat des calculs est stocké dans un tampon. Le tampon a une taille automatiquement adaptée à la définition et à la taille de l'écran utilisé. Ceci permet, après avoir sorti une image, de la refaire avec d'autres réglages de :
- Contour.
- Contour width.
- Contour top.
- Clip High et Clip Low.
Une image qui a mis deux ou trois heures à sortir, peut ainsi être redessinée avec d'autres paramètres de correspondance des valeurs aux couleurs, en quelques minutes. Rares sont les programmes qui permettent ainsi de réutiliser les valeurs calculées (le système le plus puissant que je connaisse est celui de MandelTour). Mais attention à l'encombrement de ces tampons !
Hooks : divers
On y trouve en premier lieu une perle : le hook Mandelbrot. Une fois activé, ce hook fait apparaître une fonction des plus appétissantes : Mandel(x,y,x,y,itérations,rayon).
Rayon désigne ici le "rayon de diver-gence", c'est-à-dire la valeur du module |Z| à laquelle on arrête l'itération. Non seulement c'est beaucoup plus simple que la formule récursive que nous avions donnée plus haut, mais c'est super rapide car écrit en assembleur.
La mise en service de ce "hook" offre la disponibilité de plusieurs fonctions intéressantes, qui permettent des études très poussées sur certains caractères mathématiques des fractales de Mandelbrot et Julia, mais nous ne les décrirons pas ici faute de place.
Processpixels : c'est une fonction de traitement d'image par convolution assez classique, on peut remplacer la valeur d'un pixel par une fonction pondérée des valeurs de ses voisins.
Axes : fait apparaître des axes adaptés aux types de coordonnées utilisées, rectangulaires ou polaires.
Shade : ce hook permet d'obtenir des images en perspective, avec un effet d'éclairage, ce qui les fait ressembler à des images issues d'un programme 3D. Ses effets sont limités et son maniement pas très évident. N'en obtenant rien de valable, j'ai écrit à l'auteur qui m'a envoyé le contenu d'une future note d'application, grâce à laquelle j'ai pu enfin obtenir des images qui ressemblaient à quelque chose, et certains effets surprenants. L'image principale de la couverture d'AmigaNews de décembre, ainsi que la dernière image de l'article sur les fractales paru dans ce numéro, ont été réalisées au moyen de ce "hook".

L'interface ARexx
Ce paragraphe sera bref. L'interface ARexx permet de programmer toutes les fonctions de MathVision, sauf le nombre de chiffres sur lequel il calcule, et la priorité de l'impression. Pourquoi ? Aucune idée ; après avoir lancé le contrôle de MathVision par un programme ARexx, on peut heureusement aller changer la priorité à la main en cours d'exécution. J'ai ainsi réalisé une animation de 120 images de 320x256 en haute résolution entrelacée montrant un zoom assez profond dans une fractale, les images étant ensuite montées en animation par AnimBuild.
Le programme ARexx était même fourni sur la disquette MathVision, il n'y a eu que de petites modifications à faire. Le tout s'est calculé en arrière-plan en un peu plus de 48 heures, sans anicroche.
Dernière précision : MathVision tourne sous AmigaOS 1.3 et 2.0 sans problèmes.
Conclusion
Si vous êtes intéressé par la découverte, même si vous n'êtes pas matheux, MathVision vous tiendra occupé très longtemps, tout en vous permettant de réaliser certaines images qui vous récompenseront largement de vos efforts. Ce programme combine d'une manière heureuse et performante les fonctions de bon nombre de programmes de tracé de fonctions, fractales ou non. Ses défauts sont assez mineurs, le plus gros étant la doc vraiment trop concise, et en anglais, ce qui gênera certains. Les auteurs comptent sortir d'autres "hooks" afin d'étendre continuellement les possibilités du programme.
Ma conclusion sera lapidaire. Si je devais partir avec mon Amiga sur une île déserte avec un seul programme commercial, ce serait MathVision.
|
Nom : MathVision 2.0. Développeur : Doug Houck. Éditeur : Seven Seas Software. Genre : mathématiques. Date : 1990. Configuration minimale : Amiga OCS, 68000, 1 Mo de mémoire. Licence : commercial. Prix : 197 $. |
|












