 |
Jeudi 22 janvier 2026 - 00:23 |
| Translate |
|
| Rubriques |
| Réseaux sociaux |
|
| Liste des jeux Amiga |
|
| Trucs et astuces |
|
| Glossaire |
|
| Galeries |
|
| Téléchargement |
|
| Liens |
|
| Partenaires |
|
| A Propos |
|
| Contact |
|

|
|
Maple est un logiciel de calcul formel, c'est-à-dire qu'il permet de manipuler les expressions algébriques comme (a+b)*(c+d), et d'effectuer des démonstrations. Nous vous en avions déjà parlé dans un précédent article, il est utilisé pour l'enseignement des mathématiques par Herb Brown aux Etats-Unis. Il fait partie avec LateX (pour le traitement de texte) et quelques autres logiciels, de la panoplie des outils scientifiques que l'on trouve dans la plupart des laboratoires et quelques entreprises.
Un peu d'histoire
Les logiciels de calcul formel existent depuis déjà longtemps : à l'époque où on ne connaissait guère que COBOL ou Fortran, on pouvait déjà manipuler les équations avec Macsyma et Reduce sur "mainframe"... Aujourd'hui, Mathematica est également connu car très médiatisé, mais il est moins puissant.
L'origine de Maple (érable en anglais) se trouve au groupe de calcul symbolique du département informatique de l'Université de Waterloo, dans l'Ontario (Canada), fondé en 1980. L'Université de Waterloo a encore des responsables dans son développement, mais la société qui continue à développer et maintenir Maple s'appelle Waterloo Maple Software. Il a été écrit au départ par des physiciens, pour faciliter le maniement des expressions longues et complexes qu'ils peuvent avoir à traiter. A titre d'exemple, on a pu vérifier rapidement les calculs des astronomes du XVIIe siècle concernant les mouvements lunaires, qui contiennent plus d'une centaine de termes et occupent plusieurs pages. On y a d'ailleurs découvert quelques erreurs.
Ça n'en a peut-être pas l'air, mais les problèmes auxquels est confronté un logiciel de calcul formel ("computer algebra" en anglais) sont très compliqués. Ils s'apparentent à de l'intelligence artificielle, pour la manipulation symbolique et les règles de bases, et à la reconnaissance de forme, pour appliquer ces règles à bon escient. On ne s'étonnera donc pas que ces systèmes soient souvent écrits en LISP, adapté à ce genre d'opérations.
Bien que ce que Maple permet de faire puisse paraître magique, il se comporte en élève doué ou en expert, appliquant les règles et astuces classiques (par exemple pour l'intégration ou les développements de fraction). Une opération "triviale" qui pose cependant beaucoup de problèmes est de simplifier et factoriser les expressions. Ce problème suscite encore de nombreuses recherches, car la notion de simplification a, en fait, un côté subjectif.
Les buts du calcul formel
Le calculateur formel, par essence, s'attaque à toutes les disciplines mathématiques, des plus concrètes aux plus abstraites, où les humains ont l'habitude de manipuler des symboles (algèbre, analyse, géométrie, probabilités). Au premier stade, ce genre de logiciel sait jouer avec les expressions arithmétiques, les nombres en précision infinie, et opérer quelques calculs classiques. Il est bien entendu capable de manipuler les tableaux et les matrices, par exemple pour résoudre les systèmes linéaires. On peut effectuer des démonstrations, en géométrie par exemple. On peut s'attaquer aux équations algébriques, aux systèmes non linéaires et aux équations différentielles. Comme tous les problèmes n'ont pas de solution exacte, ou facile à trouver, Maple dispose de méthodes numériques. Classiquement, on traite un problème physique de façon abstraite le plus loin possible, ce qui permet d'avoir des solutions générales. On simplifie ensuite des termes et on résout numériquement le problème.
Mais obtenir des expressions ne suffit pas toujours à rendre les choses claires au scientifique : Maple sait aussi visualiser des fonctions, en 2 ou en 3 dimensions, ainsi que les foncions implicites. Pour citer quelques autres possibilités, la manipulation des espaces mathématiques, les espaces "bizarres" comme l'algèbre de Lie non commutative, les bases de Grobner, l'optimisation de fonctions, le calcul des suites, plusieurs modules de statistiques. Dans les cas où on est intéressé par la démonstration, c'est-à-dire par le cheminement plutôt que par le résultat (ce qui en outre est intéressant pour l'enseignement), on dispose d'un mode pas à pas.
Dans la pratique, il est utile de diriger un peu Maple pour arriver a un bon résultat. Les possibilités d'écrire une expression donnée étant énormes, on a intérêt à présenter une factorisation favorable à la résolution. En effet, les cas particuliers ne sont pas toujours pris en compte, on ne peut pas toujours préciser si une variable est réelle ou complexe, ni qu'une variable doit toujours être considérée comme supérieure (ou inférieure) à une autre. Si l'on s'attaque à des problèmes complexes, on peut utiliser le langage de programmation de Maple, qui ressemble à du Pascal. Réciproquement, Maple sait écrire ses résultats sous une forme d'expression C ou Fortran.
Portage sur l'Amiga
Depuis sa création, Maple a été porté sur de nombreuses plates-formes, comme Unix (et ses nombreuses variantes), MS-DOS, Apollo, Atari, Cray, Vax, Macintosh, Silicon Graphics, et bien d'autres systèmes. De fait, on le trouve dans beaucoup d'Universités dans le monde. Nous nous intéressons bien sûr ici à son portage sur Amiga (Workbench 2.0 minimum), qui comporte quelques originalités. Un logiciel peut par exemple faire résoudre un problème par Maple en le pilotant par son port ARexx. Il est fait mention de ces particularités dans chaque documentation des différents portages de Maple.
Nous avons pu tester la version 1.0 de Maple, qui est déjà ancienne. Depuis, la version 2 est sortie. Actuellement, Maple V en est à la version 3, mais elle n'a pas été portée sur Amiga (le portage est arrêté). Dans la version 1, on dispose de deux fenêtres, une grande pour afficher les résultats et une petite pour entrer les expressions.
La fenêtre de résultat comporte un ascenseur pour revenir sur les résultats qui ont défilé hors de la fenêtre. On peut utiliser le copier/coller comme dans une fenêtre Shell. Dans la version 2, on dispose d'une fenêtre unique, dans laquelle on peut revenir modifier des expressions déjà écrites (le nouveau résultat remplace l'ancien), ce qui est très pratique. Les autres améliorations de la version 2 concernent (en bref) l'augmentation des possibilités graphiques (rendu, couleurs paramétrables par fonction, animations), un plus grand nombre de paramètres dans les courbes, et aussi quelques bogues en moins.
La version Amiga est sensée fonctionner avec 2 Mo de mémoire, mais c'est plutôt juste. On peut s'en contenter en effectuant un réglage fin du "garbage collector" (un héritage du LISP), le mécanisme qui alloue la mémoire pour les calculs, et fait le ménage régulièrement. En effet, Maple garde une trace de tous les résultats intermédiaires, pour ne pas recommencer les mêmes calculs mais aussi pour ne pas tourner en rond. L'équipe de Herb Brown s'en sert sur des A2000 avec 2,5 Mo de mémoire.
Installation
Maple se présente sous la forme de quatre disquettes et de trois gros manuels (1200 pages au total). La première disquette contient un fichier "readme" qui indique la marche à suivre pour l'installation. On y lit également qu'il s'agit de la version 0.9 de Maple V ; en fait, la commande CLI "version" nous indique qu'il s'agit bien de la version 1.0 (18.11.91). L'installation est simple : déposer le tiroir "Maple" de la disquette sur le répertoire approprié du disque dur, effectuer une assignation et exécuter le script d'installation.
L'installation prend un peu de temps (plus de 10 minutes sur ma machine) car Maple consiste en un gros exécutable accompagné d'une myriade de petits fichiers. De plus, les fichiers sont sous forme compressée sur les disquettes. L'installation prend 8 Mo et comprend plus de 3100 fichiers et répertoires. Chaque outil de Maple est implémenté dans un ou plusieurs fichiers. En fait, lorsqu'on lui demande une opération, Maple va, pour ce faire, lire un ou plusieurs fichiers, qui contiennent le code à interpréter.
Introduction au calcul
Une fois l'installation effectuée, il suffit de cliquer sur l'icône de Maple, qui représente une feuille d'érable (le symbole du Canada). Cela lance un script qui alloue 150 ko de pile avant de démarrer Maple V proprement dit. Il y a trois modes de fonctionnement : celui que nous avons décrit (deux fenêtres), dans une fenêtre Shell, et comme serveur ARexx. Lors du fonctionnement dans une fenêtre Shell, tout se passe dans cette fenêtre. Le serveur ARexx est prévu pour fonctionner en tâche de fond, sans interface utilisateur.
Maple dispose d'une copieuse aide en ligne qui permet dans beaucoup de cas de se dispenser d'aller regarder dans le manuel. Dans tous les cas, Maple ouvre un écran supplémentaire pour y afficher ses graphiques. Cet écran est en 18 couleurs, en haute résolution entrelacée pour les graphiques en 2D, et pour les graphiques en 3D, on peut changer la résolution de l'écran.
Il va être difficile de montrer les principales possibilités de Maple sans rentrer dans des considérations mathématiques, aussi allons-nous montrer des exemples simples, puis des exemples plus complexes dans certains cas. Dans un même domaine mathématique, un exemple plus complexe demandera seulement plus de temps à Maple, mais il y arrivera toujours (par exemple la dérivation). Maple échoue par exemple quand il n'y a pas de solution ou quand il n'a pas assez de mémoire pour une opération complexe. L'intérêt du calcul formel est qu'il permet de garder une expression exacte tout au long des calculs, sans passer par des approximations numériques.
Principe de fonctionnement
Commençons par un exemple classique, que la majorité d'entre vous aura rencontré au cours de ses études, a plus b au carré : (a+n)^2. En Maple, le symbole puissance s'écrit à l'aide d'un accent circonflexe ou de deux signes multipliés à la suite. Une entrée dans Maple doit toujours se terminer par un point-virgule, rentrons donc (dans la fenêtre du bas) :
| (a+b)^2; |
On aurait aussi pu rentrer (a+b)*(a+b) ou (a+b)**2. Maple nous répond dans la fenêtre du haut en réécrivant l'expression à sa façon, plus parlante.
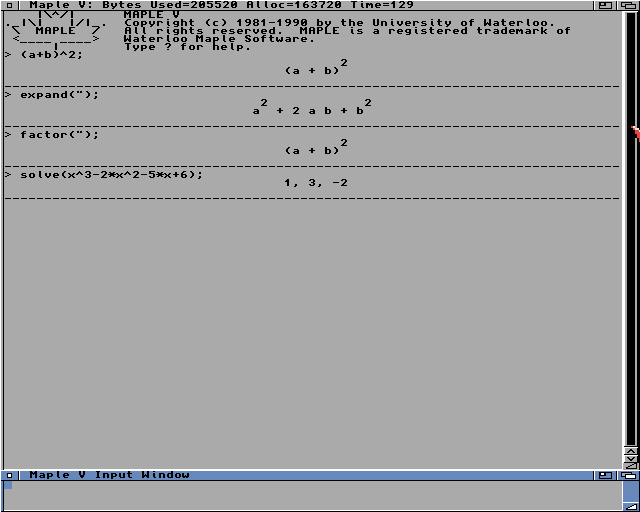
Figure 1
| expand("); |
La commande "expand()" permet de développer une expression et le signe guillemet permet de rappeler l'expression précédemment entrée. Nous obtenons le développement de notre expression, soit a^2+2ab+b^2.
Un exemple classique
Nous pouvons effectuer la fonction inverse, à savoir la factorisation. La fonction "factor()" nous le permet, entrons donc :
| factor("); |
Maple nous redonne fort logiquement (a+b)*2. Les matheux entrevoient déjà une utilisation de Maple : résoudre les équations algébriques puisque cela revient à factoriser une expression. En effet, résolvons l'expression suivante :
| 6*x^2+18*x-24; |
Tapons maintenant :
| factor("); |
On obtient :
| 6(x+4)(x-1) |
...ce qui est juste (bien sûr !) et nous donne les deux solutions : -4 et 1. Il y a cependant une fonction de Maple pour calculer directement les racines d'une équation : "solve()". Par exemple, pour compliquer un peu, calculons les racines de :
| solve(x^3-2*x^2-5*x+6); |
On obtient :
| 1,3,-2 |
A quand l'Amiga en salle d'examen ? On peut aussi résoudre des équations à plusieurs variables (des systèmes). Par exemple, trouver l'intersection de deux droites revient à résoudre le système composé des deux équations de ces droites. Soit les deux droites suivantes : x+y=1 et 2*x+y=3, la résolution est donnée par :
| solve({x+y=1,2*x+y=3},{x,y}); |
On obtient :
| {x=2,y=-1} |
...les coordonnées du point d'intersection.
Dérivées et primitives
La dérivée est une opération triviale dès lors que l'on connaît quelques formules de base. Par contre, elle peut être fastidieuse dès que l'on dérive des expressions composées, à commencer par des quotients. Entrons l'expression :
| (2*x+3)/(3*x-5); |
Là encore, Maple la réécrit façon plus classique (figure 2).
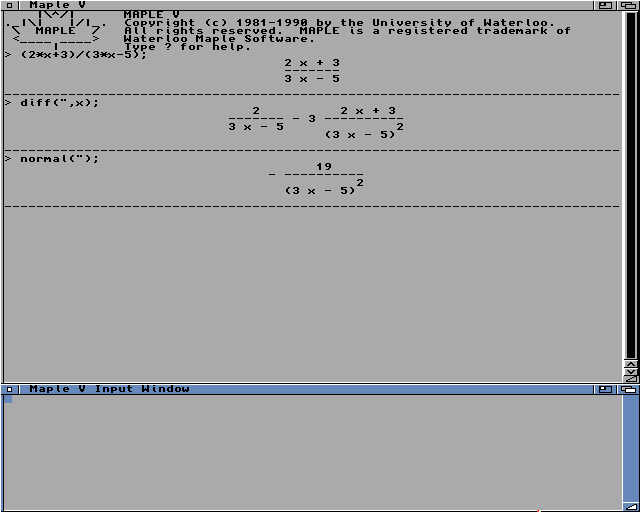
Figure 2
| normal("); |
Maple nous affiche une fraction unique, ce qui permet de conclure, quand on fait l'étude de la fonction, qu'elle est strictement décroissante (la dérivée est toujours strictement négative).
Pour obtenir la primitive (la fonction inverse de la dérivée), on utilise la fonction "int()". On peut calculer l'intégrale générale, ou le résultat de l'intégration entre deux bornes. Premier exemple, on peut calculer la primitive de 2*x+1 avec int(2*x+1,x) ce qui donne x^2+x. Deuxième exemple, on peut calculer l'intégrale de sin(x) entre 0 et Pi avec :
| int(sin(x),x=0..Pi); |
...ce qui donne 2. Dans ce cas, on obtient une valeur numérique mais si on veut la même intégrale entre 0 et 1, on obtient 1-cos(1). Pour obtenir une valeur numérique, on fait appel à la fonction "evalf(")", qui donne la valeur avec une précision de 10 chiffres par défaut : 0.4596976941. Pour obtenir 50 chiffres, on aurait rentré evalf(",50).
Dès que l'on manipule des formules nombreuses ou compliquées, on a intérêt à stocker les expressions dans des variables, comme ici :
| mafonction(x):=2*x^2+3*x+1; |
Pour la rappeler, on écrit "mafonction(x);" et pour la dériver, on écrit tout simplement "diff(mafonction(x),x);. En remplaçant "x" par une valeur numérique, on obtient la Valeur précise de notre fonction pour cette valeur de "x".
Autres caractéristiques
Nous n'allons pas détailler toutes les fonctions de base de Maple V, il y en a plus de 200. La ligne de la figure 3 montre que l'on peut obtenir les décimales de Pi (ou de racine de 2) avec une précision arbitrairement grande, il suffit d'avoir assez de temps ou de mémoire. On peut sauvegarder le contenu de la fenêtre de sortie dans un fichier, ainsi que l'imprimer.
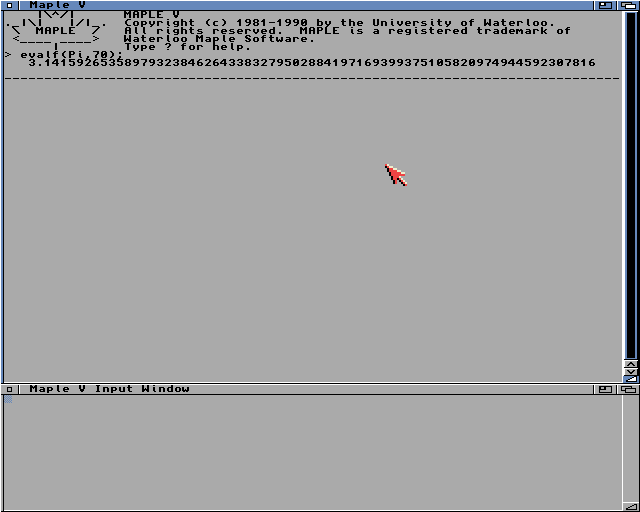
Figure 3
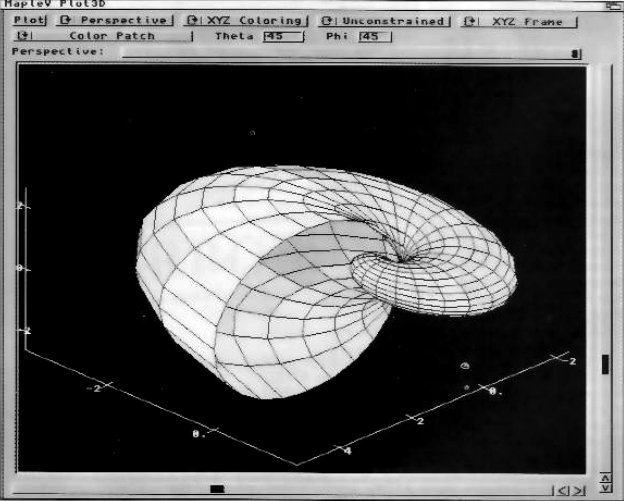
Figure 4
Enfin, Maple dispose d'une assistance très efficace, sous plusieurs formes, Waterloo Software distribue des courriers techniques (newsletter), met à disposition des correctifs et des améliorations accessibles par FTP, et il existe des conférences UseNet sur Maple. Il existe également des paquetages disponibles sur d'autres sites.
Conclusion
Nous avons vu tout l'intérêt que présente Maple, que ce soit pour la recherche classique, ou pour l'enseignement des mathématiques. Maple ne peut pas tout faire, mais il ôte le côté rébarbatif et ingrat du calcul, et en évitant les erreurs. On peut aborder des domaines théoriques avec beaucoup plus de facilité, et la visualisation permet d'explorer les fonctions de façon intuitive.
|
Nom : Maple V. Développeur : Waterloo Maple Software. Genre : mathématiques. Date : 1991. Configuration minimale : Amiga OCS, 68000, 2 Mo de mémoire, AmigaOS 2.0. Licence : commercial. Prix : 4470 FF. |
|












