 |
Mardi 27 janvier 2026 - 01:13 |
| Translate |
|
| Rubriques |
| Réseaux sociaux |
|
| Liste des jeux Amiga |
|
| Trucs et astuces |
|
| Glossaire |
|
| Galeries |
|
| Téléchargement |
|
| Liens |
|
| Partenaires |
|
| A Propos |
|
| Contact |
|

|
|
Les fractales offrent un terrain de choix pour la création de jolies images sur ordinateur ; tout les amigoïdes ou presque ont joué avec l'un ou l'autre des excellents programmes de tracé de fractales disponibles dans le domaine public, plus particulièrement ceux qui visualisent la fractale de Mandelbrot.
Programmes pour le tracé des fractales de Mandelbrot
Pour mémoire, voici quelques noms de programmes du DP :
- MandelVroom
- Mandel **
- Mandelbrot
- TurboMandel **
- MandelMountains
- MandelBlitz
- MandelPaug
- SMan
- MandAnim
- Fractals ***
- MandelTour ****
S'il y a une demande exprimée, je ferai un essai comparatif de ces programmes, en incluant ceux que je ne connaîtrais pas et dont les lecteurs intéressés me donneront les titres. Cela prendra toutefois un peu de temps, car l'essai complet de ces programmes est toujours long. J'ai une idée assez précise sur les fonctions que l'on peut souhaiter trouver dans un programme de ce genre ; aucun d'entre eux ne les a toutes, mais certains sont mieux fournis que d'autres.
Parmi les programmes commerciaux, il y a le récent FractalPro (en HAM ; je ne l'ai pas essayé, il est décrit dans AmigaWorld de mars 1991 ; il est plus orienté esthétique et animation que mathématique), le classique Doug's Math Aquarium et son digne successeur MathVision.
Les programmes de tracé de fractales par arborescence
FracGen est un programme d'initiation au tracé d'images fractales par une approche géométrique, il produit en particulier des images de végétation simples mais très réalistes.
Fractal Lab est, dans le même style, un outil moins didactique mais plus puissant.
Les programmes de tracé de paysages et assimilés
Il en existe un tout simple : Scenery ; également une version de démonstration, amputée de quelques fonctions, mais intéressante à voir, c'est Genesis.
Il y a dans ce domaine une série de programmes commerciaux, donnant des images utilisables professionnellement, comme Vista Pro. Cinq de ces programmes ont fait l'objet d'une présentation dans AmigaWorld de juillet 1991. Les notions présentées ici ont été extraites de divers ouvrages dont les références seront données en fin d'article.
Qu'est-ce qu'une fractale ?
Prenons un exemple, illustré au moyen du programme FracGen.
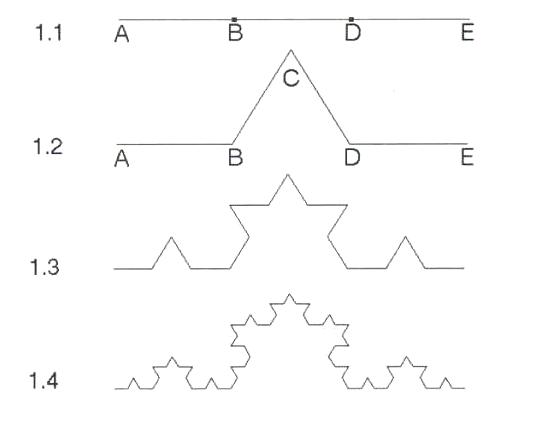
Figure 1
Nous obtenons quelque chose qui commence à ressembler à un flocon de neige et qui s'appelle la fractale de Von Koch. Cette construction apparemment simple a pourtant une propriété étonnante : si on continue l'opération ci-dessus indéfiniment, la longueur de la ligne obtenue tend vers l'infini. C'est facile à comprendre : admettons que le segment AE du début mesure 3 cm. La ligne brisée (1.2) mesure 4 cm, soit les 4/3 de AE. De même, chacune des lignes brisées construite sur un segment de (1.2) est plus longue que ce segment, dans le même rapport de 4/3. La ligne 1.3 est donc plus longue que la ligne 1.2.
Chaque fois que nous effectuons une nouvelle itération, la longueur de la ligne qui relie A à E augmente d'un tiers. Or le produit répété d'un nombre par lui-même tend vers l'infini lorsque ce nombre est plus grand que 1. Nous sommes donc capables de construire entre deux segments une ligne brisée de longueur aussi grande que nous le voulons !
Amusement de mathématicien ?
Non, la nature nous offre des situations similaires. Partons en Bretagne du Nord, du côté de l'île de Bréhat, et essayons de mesurer la longueur de la côte d'une île entre deux points. Prenons un mètre pliant et au travail, sans nous poser trop de questions. Nous trouvons par exemple 1257,252 mètres. Oui, mais notre mètre pliant n'a pu se plier à toutes les anfractuosités de la côte. Bon, on prend un mètre ruban et on recommence.
On obtient bien entendu une longueur plus grande. Mais même notre mètre ruban ne peut pas suivre tous les détails du contour. Tant pis, faisons des photos couvrant une surface de 1 mètre par un mètre et travaillons sur les agrandissements. Peste, ce n'est pas encore ça ! En effet, plus nous agrandissons, plus nous trouvons de détails, et plus la mesure de notre côte s'allonge. Notre côte se comporte donc en quelque sorte à la manière de la courbe de Von Koch. Tout ceci ne nous dit toujours pas pourquoi on appelle cela une fractale.
Retournons à notre brave FracGen et refaisons l'exercice en divisant différemment notre segment.
Nous constatons qu'à mesure que le nombre d'itérations augmente, la courbe 2 couvre une partie du plan plus importante que la courbe 1.
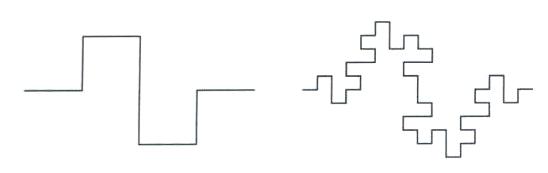
Figure 2
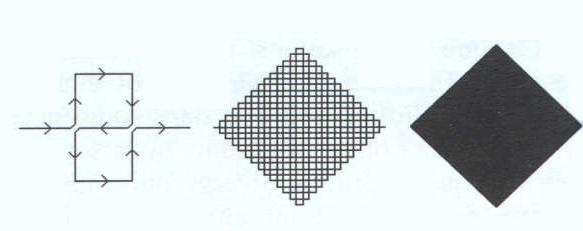
Figure 3
Pour la courbe 1 : D=log(4) / log(3)=1,26...
Pour la courbe 2 : D=log(8) / log(4)=1,5
Pour la courbe 3 : D=log(9) / log(3)=2
C'est le fait que ces courbes peuvent avoir des dimensions fractionnaires qui les a fait appeler fractales. Il y a moyen également d'obtenir des figures fractales de dimension inférieure à l'unité. Prenons un segment, divisons-le en 3 et enlevons le segment du milieu. Recommençons cette opération sur les deux segments qui restent et ainsi de suite. Le pointillé que l'on obtient ainsi s'appelle une poussière de Cantor ; l'application de la formule ci-dessus lui attribue une dimension de 0.6309...
Autosimilarité et autosimilitude
Les fractales ont une propriété d'autosimilarité, c'est-à-dire que lorsqu'on les regarde avec des grossissements de plus en plus forts, on retrouve des motifs similaires, et ceci aussi loin que la puissance de l'ordinateur permet de descendre. Celles que nous avons examinées aujourd'hui ont même une propriété d'autosimilitude, le grossissement révélant des motifs identiques, seule la taille étant différente, et ceci à l'infini.
Dans la nature, on trouve beaucoup de choses qui ont un caractère fractal ; nous avons déjà cité l'exemple d'une côte. Les ramifications d'une fougère ou d'un flocon de neige en sont d'autres exemples.
Benoît Mandelbrot a même écrit un ouvrage célèbre à ce sujet "La Géométrie Fractale De La Nature". Toutefois, les constructions naturelles ont deux différences fondamentales avec nos constructions mathématiques : les fractales naturelles n'ont jamais complètement la propriété d'autosimilitude, mais seulement d'autosimilarité. Lorsque l'on grossit, on trouve des choses similaires, mais non pas semblables au sens des triangles semblables de la géométrie. L'autre différence est le fait que dans la nature, la division fractale s'arrête toujours à un certain niveau ; l'infiniment petit n'existe pas. A un moment donné on trouve la molécule ou l'atome et c'est fini. Généralement la division fractale s'arrête assez vite, voir de nouveau la fougère.
Il est intéressant de constater que notre outil d'investigation, c'est-à-dire l'ordinateur, est aussi soumis à cette limitation, à la fois par le nombre de décimales avec lesquelles il peut effectuer un calcul, et par la résolution de l'affichage. Dans le cas de la fractale de Von Koch, sur un écran 640x512, au-delà de sept itérations, on ne constate plus aucune différence, et on constate que les bords du trait deviennent chaotiques.
La compréhension de certaines caractéristiques des fractales va permettre d'entrevoir les voies nouvelles vers laquelle la physique se dirige depuis quelques années, avec l'étude des relations entre l'ordre et le chaos.
Paysages
Écrivons un bout de programme qui dessine une fractale de Von Koch, avec un niveau de fractalisation de 4 ; chaque fois que nous tracerons un segment, faisons varier aléatoirement sa longueur dans une certaine limite (plus ou moins 50%) et appliquons également une variation aléatoire à l'angle entre un segment et le suivant (normalement un multiple de 60 degrés). Nous obtenons à chaque exécution une courbe différente. Ajoutons un cadre et un remplissage en gris, et nous obtenons quelque chose qui, malgré des imperfections évidentes dues au peu de sophistication de notre procédé, ressemble néanmoins à une côte.
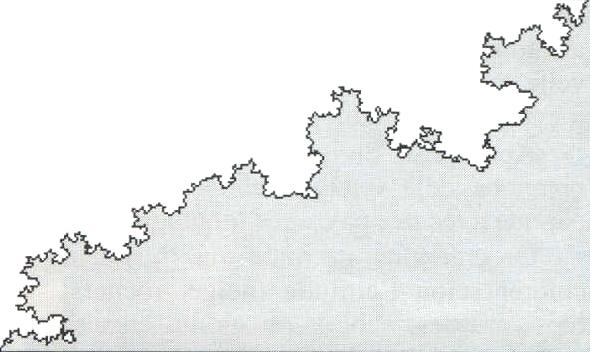
Figure 4
Doublons la densité de la grille. Nous avons maintenant deux choix : soit affecter une altitude aléatoire à chaque nouveau point, soit calculer un nombre aléatoire pour tous les points de la nouvelle grille, et additionner ces compléments d'altitude aux points déjà existants. Après deux divisions de la grille, nous obtenons déjà quelque chose qui a une parenté avec des paysages montagnards.
On crée ainsi un relief que l'on peut colorer selon l'altitude (neige, rochers, bois, prairies, sable) ; on ajoute ensuite des lacs bleus dans les cuvettes du relief ; entre ces cuvettes on trace des rivières. On obtient ainsi des paysages qui deviennent assez réalistes.
La figure 5 a été obtenue avec le programme Scenery. C'est un vieux programme et l'image n'est pas terrible, mais au-dessus de 3000 m, on trouve des paysages de ce genre. Sur Fish 216, on trouve un programme nommé Cloud, qui produit des nuages fractals assez réalistes.

Figure 5
Considérons une droite "0x". Elle comporte un point particulier, le point "A" d'abscisse "1". Prenons un nombre inférieur à l'unité, c'est-à-dire, représenté par un point compris entre "0" et "A". Si on le multiplie par lui-même, puis le résultat par ce nombre, etc. (autrement dit si on en prend les puissances successives), le résultat tend vers zéro quel que soit le nombre choisi. On dit que zéro est un attracteur pour ce type d'itération, dans ce domaine de la droite.
De même, quel que soit le nombre choisi à droite de A, le résultat de l'itération tend vers l'infini. Il y a donc, pour ce type d'itération, deux attracteurs, zéro et l'infini, séparés par une frontière qui est le nombre 1.
Étendons ceci au plan complexe x,y. Si nous prenons un nombre complexe dont le module est inférieur à 1, c'est-à-dire représenté par un point situé à l'intérieur d'un cercle de rayon 1 centré sur l'origine, les puissances successives de ce nombre complexe ont un module qui tend vers zéro. A l'extérieur du cercle, elles tendent vers l'infini. Le plan sera donc découpé en deux régions, chacune possédant un attracteur, et séparées par une frontière. Vous serez d'accord avec moi qu'il n'était pas nécessaire d'illustrer ceci par un dessin !
Frontières chaotiques
Au lieu de prendre un brave nombre complexe :
Z0=x+i*y
...et d'effectuer l'itération :
Zn=(Zn-1)^2 (puissances paires), essayons l'itération :
Zn=(Zn-1)^2 + C, où C est une constante complexe a+i*b.
Si vous n'aimez pas les nombres complexes, considérez simplement que l'expression Z=a+i*b correspond à un point "P" du plan, de coordonnées "a" et "b". "a" correspond à ce qu'on appelle la partie réelle du nombre complexe, "b" à sa partie imaginaire, et le module |Z|, égal à la racine carrée de a^2+b^2, représente tout simplement la distance du point "P" à l'origine.
Eh bien, dans ce cas-ci, bien que l'on puisse pressentir que pour certaines valeurs C, l'itération tendra vers une limite finie, et pour d'autres, vers une limite infinie, il n'y a aucun moyen analytique d'obtenir l'équation de la frontière. Il faudra, pour chaque point du plan, faire un certain nombre d'itérations, et observer si le module de notre résultat tend vers quelque chose. C'est ce qu'a fait Benoît Mandelbrot au début des années 1980 ; vu qu'il travaillait chez IBM, les moyens de calcul ne manquaient pas.
Au début du siècle, les Français Julia et Fatou avaient bien découvert de nombreuses propriétés de l'itération d'une variable complexe, mais le manque de nos moyens de calcul modernes les avaient empêchés de les traduire visuellement, ce qui était un gros handicap.
La fractale de Mandelbrot
L'idée de base est de prendre pour chaque point du plan, ses coordonnées "x" et "y", et d'effectuer un certain nombre d'itérations du type décrit ci-dessus, et de surveiller le module du résultat, que nous appellerons |Z|. Dans le cas de la fractale de Mandelbrot, la constante complexe vaut x+i*y, elle est donc différente pour chaque point du plan. Lorsque l'on utilise pour C une constante complexe, on obtient une fractale de Julia.
Les mathématiciens ont pu démontrer que dès que |Z| dépasse 2, la suite des itérations est certainement divergente, c'est-à-dire. que |Z| tendra vers l'infini. Dès que |Z| dépasse 2, on arrête le calcul, et on colore le pixel correspondant en blanc. Par ailleurs, comme on ne peut évidemment pas faire un nombre infini d'itérations, on se fixe arbitrairement une limite, par exemple 100 itérations. Si au bout de 100 itérations, |Z| n'a pas dépassé 2, on déclare que le point fait partie de l'ensemble de Mandelbrot et on le colore en noir. Le résultat d'une telle opération est donné à la figure 6, pour 1000 itérations, la portion du plan balayée va de -1 à 2 en "x" et de -1,2 à 1,2 en "y". L'écran est en 640x512.

Figure 6

Figure 7
Mais la présence des petites taches nous fait penser qu'il y a sans doute des choses intéressantes à voir. La partie blanche des figures 1 et 2 correspond à des points pour lesquels |Z| a dépassé 2 en moins de 1000 itérations, mais en combien exactement ? Demandons à notre programme de tracé de colorer les pixels en 10 nuances de gris, selon qu'il a fallu 1, 2, 3, etc. itérations. Nous nous limitons dans ce cas à 50 itérations, c'est suffisant pour ce que nous voulons voir. Nous commençons à obtenir une représentation classique de la fractale de Mandelbrot (figure 8).
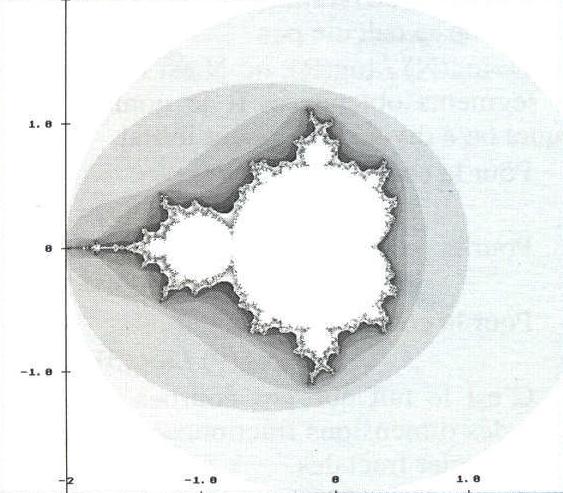
Figure 8
Mais, comme vous le savez déjà, toute cette zone proche de l'ensemble de Mandelbrot révèle une complexité et une beauté de formes tout à fait inattendues de la part d'une fonction dont l'expression est aussi simple. En faisant des zooms de plus en plus grands, et en augmentant progressivement le nombre d'itérations, on constate à la fois une répétition des mêmes motifs, mais aussi une diversité de plus en plus grande de ces motifs.
Dans les branches du dessin, on voit apparaître des réductions de l'ensemble de Mandelbrot initial (figure 9), orientées selon des angles divers, donnant elles-mêmes des branches à motifs de plus en plus compliqués. A d'autres endroits, on peut zoomer tant que l'on veut, le dessin reste identique à lui-même. L'analyse de ces formes a été faite sous toutes les coutures par les mathématiciens, ceux que cela intéresse trouveront l'information dans les ouvrages mentionnés dans la bibliographie. Les images de fractales de Mandelbrot sont assez connues, mais le plaisir de découvrir des motifs nouveaux reste entier, et, comme nous l'avons déjà signalé, il y a de nombreux programmes commerciaux ou du DP pour le faire.
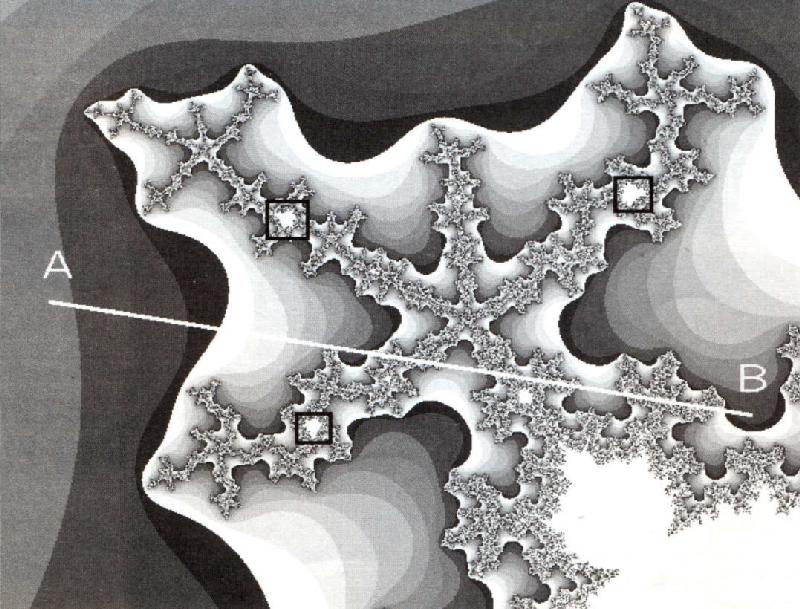
Figure 9
L'ordre intérieur
A l'extérieur de la frontière de l'ensemble de Mandelbrot, qui a, comme nous l'avons vu, l'allure d'une courbe fractale, nous sommes dans le domaine de l'attracteur infini, de la divergence. Au voisinage de la frontière, nous sommes en plein chaos. Et à l'intérieur, qu'y a-t-il ?
Vu que l'intérieur (la partie noire de la figure 6) est composé des points pour lesquels il n'y a pas eu de divergence avant le nombre d'itérations que nous nous sommes fixés arbitrairement, par exemple 100, nous pouvons nous demander ce qui est arrivé au module |Z| au moment où nous avons touché la centième itération. Et que se serait-il passé si nous avions fait 10 ou 10 000 itérations ?
Eh bien, faisons un petit programme ou utilisons un outil comme MathVision pour calculer, pour un point donné du plan, la valeur du module |Z| pour un nombre d'itérations allant par exemple de 1 à 100.
Nous constatons alors que les choses sont nettement différentes. Dans une région centrale, les valeurs successives |Z| oscillent mais ces oscillations décroissent et se stabilisent à une valeur donnée. Cette valeur est différente pour chaque point, on ne peut pas dire qu'il y ait un attracteur. Au fur et à mesure que l'on se rapproche des bords de l'ensemble, on constate que dans certaines zones le module effectue des oscillations qui se stabilisent autour de deux valeurs, puis de trois, etc. Lorsque l'on se rapproche encore de la limite, le tracé des oscillations successives devient de plus en plus complexe, et tout-à-coup, lorsque l'on passe la frontière, l'oscillation diverge.
On ne voit pas souvent d'images représentant l'intérieur de l'ensemble de Mandelbrot, car en général elles ne donnent pas lieu à des créations artistiques aussi frappantes que les images classiques de l'extérieur. Cependant, ce qui s'y passe est important, car nous passons d'un domaine "calme" et "ordonné" les itérations de |Z| se stabilisent autour de quelques valeurs finies, les zones de |Z| constant sont des cercles assez peu déformés (voir figure 10), au domaine du chaos, en franchissant une frontière qui est une fractale.

Figure 10
Un système complexe, mis "sous pression" (par exemple la circulation à Paris lorsque le trafic augmente), passe d'un régime assez linéaire en cas de faible trafic à un régime chaotique avec des arrêts et des fonctionnement fluides peu prédictibles. Il peut d'ailleurs sortir à certains moments de ce chaos et trouver un équilibre, comme notre itération dans les petits Mandelbrots de deuxième génération, mais, d'une manière similaire, la marge de stabilité est étroite et la moindre perturbation le fait replonger dans l'état chaotique.
De même, alors que l'on croyait que le fait de disposer d'un nombre suffisamment grand de stations de mesure et d'ordinateurs suffisamment puissants permettrait de faire des prévisions météorologiques locales à long terme, on sait maintenant qu'il n'en est rien. Le système de l'atmosphère est turbulent et chaotique, ce n'est pas un hasard si les barbules de certains nuages nous font penser à des circonvolutions de la fractale de Mandelbrot.
Bon, trêve de considérations philosophiques, mais le fait est qu'un micro-ordinateur doté de bonnes capacités graphiques comme l'Amiga, et de programmes du genre de MathVision, peut vous permettre d'aborder intuitivement et analytiquement certains concepts qui sont en train de révolutionner la physique, en attendant d'être appliqués à la conduite de systèmes complexes d'un autre genre, comme la direction des sociétés ou l'économie. Avec en prime la création de jolies images.
La fractale de Julia
La fractale de Julia a ceci d'intéressant que son aspect dépend de la valeur de la constante fixe C=a+i*b, et que ses changements d'aspects sont étroitement liés à la position du point de coordonnées "a" et "b", par rapport à la fractale de Mandelbrot. Pour un point situé à l'intérieur de l'ensemble, la fractale de Julia possède une frontière fractale mais continue. Lorsque C correspond à un point situé hors de l'ensemble de Mandelhrot, la fractale de Julia explose en nuages de poussière du plus bel effet.
À propos, saviez-vous que l'on peut trouver des osselets dans une fractale de Julia ?
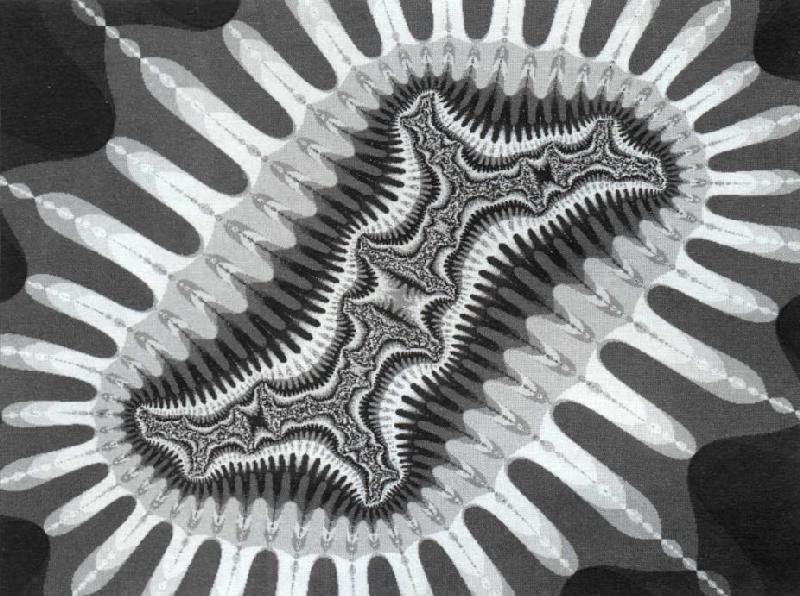
Figure 11
Rassurez-vous, on arrive au bout ! Non que le sujet soit épuisé, il y a beaucoup de sortes de fractales basées sur des itérations, le programme Fractals donne quelques informations à ce sujet dans sa documentation. Des procédés comme la recherche des zéros d'une fonction complexe par ma méthode de Newton donnent également de jolies images, d'aspect parfois étrangement biologique.
Nous avons survolé, vraiment très vite, un domaine extrêmement large. Si certains d'entre vous sont restés sur leur faim, j'ai atteint mon but. Une revue est là pour présenter des sujets, elle ne peut pas se substituer à des livres entiers !
Pour ceux qui voudraient approfondir l'étude des fractales, je recommande trois ouvrages :
- Benoît Mandelbrot : The Fractal Geometry of Nature. Freeman.
- H.-O. Peitgen et Richter : The Beauty Of Fractals. Springer Verlag.
- Des mêmes auteurs : The Science of Fractal Images. Springer Verlag.
Enfin, si les notions de passage de l'ordre au chaos et réciproquement vous intéressent, je vous recommande aussi :
- J. Briggs et F. Peat : Un Miroir Turbulent (sous-titré "Un guide illustré de la théorie du chaos"). InterEditions FNAC, même rayon.

Figure 12
|












