Suivez-nous sur X
|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement
|
|
David Brunet
|
|
|
|
Programmation : C - Préprocesseur générant des objets filaires pour Anim
(Article écrit par Pascal Amiable et extrait d'Amiga News Tech - novembre 1990)
|
|
Chers lecteurs et lectrices, bonjour. Ce mois-ci, je vous propose de réaliser un préprocesseur d'objets pour le
programme d'animation en filaire "Anim" que nous avons étudié ensemble il y a
deux mois. Ce préprocesseur va nous décharger de la fastidieuse
opération de création d'objets puisqu'il va générer les fichiers de points et de lignes à partir de quelques
données de base. Pour étayer mon propos, je vous propose un exemple de programme qui va générer un tore.
Avant d'étudier cet exemple de préprocesseur, je vais effectuer un bref rappel sur la structure des fichiers
de points et de lignes qui composent notre objet. Le fichier de points (point.dat) contient la liste des
coordonnées X,Y,Z de chaque point 3D de l'objet. Sa structure est la suivante :
- 1re ligne <N> (nombre de points)
- 2e ligne <X1> <Y1> <Z1> (coordonnées du 1er point)
- 3e ligne <X2> <Y2> <Z2> (coordonnées du 2e point)
- ...
- N+1re ligne <Xn> <Yn> <Zn> (coordonnées du Ne point)
Le fichier de lignes (ligne.dat) contient, quant à lui, les numéros des points origines et extrémités
de chaque segment composant l'objet. Sa structure est la suivante :
- 1re ligne <M> (nombre de lignes)
- 2e ligne <Origine1> <Extrémité1> (1er segment)
- 3e ligne <Origine2> <Extrémité2> (2e segment)
- ...
- M+1re ligne <OrigineM> <ExtrémitéM> (Me segment)
Ce petit rappel effectué, nous allons passer aux choses sérieuses. L'idée de départ consiste à générer un
objet complexe à partir d'un nombre restreint de données à l'origine. L'exemple que nous allons étudier
est celui d'un tore. Un tore est défini mathématiquement par trois nombres, R1 représente le petit rayon
du tore, R2 représente le grand rayon (ou rayon central) du tore et n le nombre de points également répartis
sur le cercle central et sur le petit cercle.
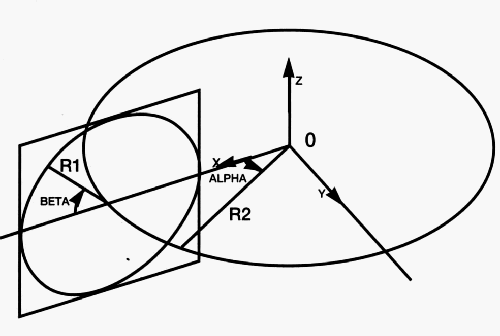Figure 1
La première étape de la programmation va consister à générer le fichier de points. Il nous faut calculer pour
commencer le nombre de points de l'objet. C'est très simple puisque n représente à la fois le nombre de points
répartis sur le petit cercle et le grand cercle. Le nombre de points total de l'objet est dont n*n.
Nous allons maintenant calculer les coordonneés X, Y, Z de chaque point de l'objet. Le grand cercle du tore a
pour équation paramétrique :
X2 = R2*cos(alpha)
Y2 = R2*sin(alpha)
Z2 = 0
|
Ces coordonnées X2,Y2,Z2 représentent également les coordonnées des centres des petits cercles de notre tore.
Dans le cas où alpha vaut zéro les équations d'un point appartenant au petit cercle sont :
x = R1*cos(beta)+R2
y = 0
z = R1*sin(beta)
|
Lorsque alpha varie décrivant notre tore, on calcule facilement les coordonnées d'un point quelconque de ce
tore en multipliant les coordonnées (x,y,z) ramenées en alpha = 0 par une matrice de rotation d'axe z
et d'angle alpha. Ce qui nous donne les équations suivantes pour les coordonnées d'un point (X',Y',Z')
d'un point du tore :
X' = x*cos(alpha)
Y' = x*sin(alpha)
Z' = z
|
Nous avons là tous les éléments nécessaires à la génération du fichier de points. Ce problème étant réglé, nous
allons nous pencher sur la manière dont nous allons relier ces points par des segments et ainsi créer notre objet.
Il s'agit de la création du fichier "ligne.dat".
Pour chaque segment de notre tore, il faut déterminer les numéros des points origines et extrémités le caractérisant.
Le maillage du tore s'effectue en deux étapes. Chaque petit cercle du tore est défini par n points, ces points
sont connectés entre eux par n segments représentés par des couples de points. Par exemple, pour le premier petit
cercle ces couples sont (j,j+1), j variant de 0 à n-2, le couple (n-1,0) clôturant le cercle. Pour un cercle
quelconque i, les couples sont (i*n+j,i*n+j+1), j variant toujours de 0 à n-2. Le segment de clôture est dans ce cas
(i*n+n-1,i*n). L'algorithme de création des segments associés aux petits cercles se détermine à partir des constatations
ci-dessus.
Nous avons donc tous les segments associés aux petits cercles, il s'agit donc d'en faire de même pour les segments liés
aux grands cercles. Pour le premier grand cercle un segment est défini par un couple (i*n,i*n+n), i variant de 0 à n-2.
Le segment de clôture du cercle associé est (n*(n-1),0). Pour un grand cercle quelconque, ce couple devient (i*n+j,i*n+j+n)
avec en clôture (n*(n-1)+j,j). L'algorithme de calcul de ces différents couples est donc :
Dernier point à déterminer : le nombre de segments liés à un objet. Nous avons n*n segments liés aux petits cercles
et autant pour le grand cercle. Le nombre de segments total est donc 2*n*n.
A partir de toutes ces explications, il est très facile de réaliser un petit programme en C qui génère ce tore.
Les fichiers tpoint.dat et tigne.dat pouvant être ensuite relus par le programme Anim afin d'être visualisés à
l'écran. Une petite remarque toutefois ; n'oubliez pas de redimensionner les tableaux de points et de lignes du
programme Anim en fonction des objets que vous allez manipuler.
/* ---------------------------------------------------------- */
/* */
/* Préprocesseur générant des objets filaires pour ANIM */
/* */
/* Cet exemple génère un Tore */
/* */
/* P. AMIABLE */
/* */
/* ---------------------------------------------------------- */
#include <stdio.h>
#include <math.h>
main()
{
FILE *fp, *fopen ();
float R2,R1,alpha,beta,delta,x;
int n,i,j;
/* SAISIE DES DONNEES n,R2,R1 PERMETTANT LA DESCRIPTION DU TORE */
printf("Nombre de rotation sur le tore : ");
scanf("%d",&n) ;
printf("Valeur du rayon du grand cercle : ");
scanf("%f",&R2);
printf("Valeur du rayon du petit cercle : ") ;
scanf("%f",&R1);
/* OUVERTURE DU FICHIER DE POINTS */
if(!(fp = fopen("tpoint.dat","w"))) exit();
delta = 2.0*PI/n; /* CALCUL DU PAS DE ROTATION */
fprintf(fp,"%d\n",n*n); /* NOMBRE DE POINTS DE L'OBJET */
/* CALCUL DES COORDONNEES DES DIFFERENTS POINTS */
for(i=0;i<n;i++)
{
alpha = i*delta;
for(j = 0;j<n;j++)
{
beta = j*delta;
x = R2+R1*cos(beta);
fprintf(fp,"%f %f %f\n",cos(alpha)*x,sin(alpha)*x,R1*sin(beta));
}
}
fclose(fp);
/* OUVERTURE DU FICHIER DE LIGNES */
if(!(fp = fopen("tligne.dat","w"))) exit();
fprintf(fp,"%d\n",n*n*2); /* NOMBRE DE LIGNES DE L'OBJET */
/* CALCUL DE LA PREMIERE SERIE DE LIGNES (PETITS CERCLES) */
for(i=0;i<n;i++)
{
for(j = 0;j<n-1;j++)
fprintf(fp,"%d %d\n",i*n+j,i*n+j+1);
fprintf(fp,"%d %d\n",i*n+j,i*n);
}
/* CALCUL DE LA DEUXIEME SERIE DE LIGNES (GRANDS CERCLES) */
for(j=0;j<n;j++)
{
for(i = 0;i<n-1;i++)
fprintf(fp,"%d %d\n",i*n+j,i*n+j+n);
fprintf(fp,"%d %d\n",n*(n-1) + j, j) ;
}
fclose(fp);
}
|
Mise à jour de mai 2025 : une archive contenant le listing adapté à vbcc, et avec l'exécutable
compilé par vbcc, a été réalisée par Yann-Gaël Guéhéneuc et est disponible sur
obligement.free.fr/files/ant3dgraphicspreprocessorverticesanim.lha.
|
