Suivez-nous sur Mastodon

|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement

|
|
David Brunet

|
|
|
|
Programmation : C - Les objets complexes en 3D
(Article écrit par Thomas Landspurg et extrait d'Amiga News Tech - mai 1992)
|
|
Afficher des objets complexes en 3D, c'est bien. Les animer, c'est mieux. Et plus difficile, aussi.
Il y a plusieurs types d'animations, la plus simple consistant à uniquement faire bouger l'objet dans l'espace.
Mais c'est un peu juste si l'on veut aller plus loin et animer des objets complexes. Le type d'animation que
nous allons voir consiste à dire qu'un objet est formé de plusieurs sous-objets, mobiles entre eux.
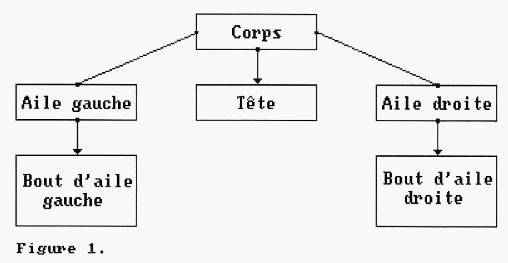
Prenons comme exemple un oiseau. Pour l'animer, prenons comme point de départ le corps. On aurait ensuite les
ailes et la tête, qui sont liées au corps mais mobiles par rapport à lui. C'est-à-dire que si le corps bouge,
les ailes bougent aussi, mais les ailes peuvent aussi bouger de manière relative au corps (Cf. figure 1).
Ensuite, on a les extrémités des ailes, évidemment liées aux ailes elles-mêmes, mais également mobiles par rapport
à elles. Il s'agit d'une construction hiérarchique, où chaque élément dépend du précédent. Cette organisation
est bien connue des utilisateurs de Sculpt et autres modeleurs.
Il faut donc créer une structure de données qui puisse refléter cette hiérarchie. La structure objet comporte les
éléments classiques pour un objet en 3D :
- Les angles (ax, ay, az) et les positions relatives (cx, cy, cz) de l'élément.
- Le nombre de points de cet élément (nb_pt).
- Un pointeur sur les coordonnées des points qui composent cet élément (p_pt).
- Le nombre de lignes (nb_lines).
- Un pointeur sur le tableau des numéros des points de début et de fin qui forment
les lignes de l'élément (p_lines).
Jusqu'à présent, rien que de très classique, mais c'est là que cela devient intéressant : on a aussi
un pointeur sur un tableau contenant la liste des sous-éléments liés à cet élément (p_tab).
En reprenant l'exemple de l'oiseau, à l'élément corps serait associé un tableau de pointeurs contenant
les adresses des éléments ailes et tête. Chaque sous-élément peut lui-même être père de plusieurs autres
éléments. Mais n'oublions pas que nous sommes en 3D temps réel et qu'il faudra bien se limiter à un
moment ou à un autre, pour des questions de vitesse d'affichage.
Le programme
Une fois n'est pas coutume, il est écrit en C. Il n'y a pas de problème majeur à sa transcription en assembleur,
mais il faut noter que le C se débrouille de manière très honorable question vitesse.
Le programme alloue deux écrans d'un plan de bits chacun pour le double tampon mémoire, puis les affiche
alternativement. L'affichage de l'objet se fait de manière récursive dans la procédure "Aff_Obj".
On commence par afficher le premier élément : calcul des rotations, passage de 3D en 2D et affichage.
Ensuite, on appelle de nouveau la procédure Aff_Obj pour chacun des sous-éléments de l'élément courant, en
additionnant ses angles de rotations et ses déplacements relatifs à ceux du père.
Note : Il y a une petite astuce pour l'affichage des lignes. Un couple (1, 3) indique qu'il faut
tracer une ligne entre le point numéro 1 et le point numéro 3 de l'élément courant, mais un couple (1, -3)
indique un tracé entre le point 1 de l'élément courant et le point 3 de l'élément précédent (c'est-à-dire
l'élément père). Cela permet de tracer des lignes entre des points de l'élément père et de points de l'élément courant.
Seul problème, le point de numéro 0 n'a pas d'opposé (-0 =0). On indique alors ce cas particulier en
utilisant la valeur -MAX PT comme numéro de point.
Le listing ci-dessous contient comme exemple un oiseau battant des ailes. L'exemple d'utilisation est
relativement simple et n'utilise pas toutes les possibilités de cette technique. A vous donc de trouver
de superbes objets à animer, mais avant de vous lancer dans l'aventure, je vous conseille d'essayer de
bien comprendre la structure des données.
/* Move par T.Landspurg */
/* A compiler avec "lc -Lm move" */
#include "exec/types.h"
#include <graphics/gfxbase.h>
#include <graphics/view.h>
#include <graphics/rastport.h>
#include <math.h>
USHORT quit_flag = FALSE;
long IntuitionBase=0;
struct GfxBase *GfxBase=0;
struct Window *OpenWindow();
struct Screen *OpenScreen();
#define DEPTH 1
#define WIDTH 320
#define HEIGHT 256
#define MAX_PT 30
UWORD ColorTable[]={0,0xf0};
typedef struct pt{
int x,y,z;
};
typedef struct line{
int deb,fin;
};
typedef struct pt_2d{
int x,y;
};
typedef struct obj{
int nb_pt; /* Nombre de pt de l'element */
int nb_lines; /* nombre de lignes */
int ax,ay,az; /* Angles relatifs */
int cx,cy,cz; /* Deplacements relatifs */
struct pt *p_pt; /* tableau des pts de l'elem */
struct line *p_lines; /* tableau des lignes */
struct obj **p_tab; /* tableau des elements fils */
};
/* LA TETE */
struct pt pt_tete[]={{-10,10,0},{10,10,0},{0,0,20},{0,5,0}};
struct line lines_tete[]={{0,1},{1,2},{2,0},{0,3},{1,3},{2,3}};
struct obj tete={4,6,0,0,0,0,0,40,pt_tete,lines_tete,NULL};
/* LES AILES ET BOUTS D'AILES */
struct pt pt_aile[]={ {20,0,30},{20,0,0} };
struct pt pt_aile_bord[]={ {20,0,25},{20,0,5} };
struct line lines_aile_bord[]={ {0,-MAX_PT},{1,-1},{0,1} };
struct line lines_aile[]={ {0,-3},{1,-2},{0,1} };
struct line lines_aile2[]={ {1,-1},{0,-MAX_PT},{0,1} };
struct obj aile_bord={2,3,0,0,100,20,0,0,pt_aile_bord,lines_aile_bord,NULL};
struct obj aile_bord2={2,3,0,0,-100,20,0,0,pt_aile_bord,lines_aile_bord,NULL};
struct obj *tab_aile_bord[]={&aile_bord,NULL};
struct obj *tab_aile_bord2[]={&aile_bord2,NULL};
struct obj aile1={2,3,0,0,0,10,0,0,pt_aile,lines_aile,tab_aile_bord};
struct obj aile2={2,3,0,0,180,-10,0,0,pt_aile,lines_aile2,tab_aile_bord2};
/* LE CORPS */
struct pt pt_corps[]={
{-10,10,30},{-5,10,-30},{5,10,-30},{10,10,30},{0,-5,10}
};
struct line lines_corps[]={
{0,1},{1,2},{2,3},{3,0},{4,0},{4,1},{4,2},{4,3}
};
struct obj *tab_corps[]={&aile2,&aile1,&tete,NULL};
struct obj corp={5,8,0,0,0,0,0,0,pt_corps,lines_corps,tab_corps};
int de=200; /* distance de l'ecran a l'observateur */
int d=600; /* distance de l'observateur au pt 0 */
int t_cos[360]; /* tables de sinus et cosinus */
int t_sin[360];
/********************* Rotation dans le plan ************/
void rot(angle,p_x,p_y)
int angle,*p_x,*p_y;
{
int x,y;
x= (*p_x)*t_cos[angle]+(*p_y)*t_sin[angle];
y=-(*p_x)*t_sin[angle]+(*p_y)*t_cos[angle];
*p_x=x>>8;
*p_y=y>>8;
}
/***************** Calcul de la projection 3D->2D ******/
void calc_coord(p_pt,p_x,p_y)
struct pt *p_pt;
int *p_x,*p_y;
{
if(d+p_pt->z!=NULL){
*p_x= WIDTH/2+(p_pt->x*de)/(d+p_pt->z);
*p_y=HEIGHT/2-(p_pt->y*de)/(d+p_pt->z);
}
}
/************** Affichage de l'objet ******************/
void AffObj(rp,p_obj,ax,ay,az,ox,oy,oz,old_pt)
struct RastPort *rp;
struct obj *p_obj;
int ax,ay,az;
int ox,oy,oz;
struct pt_2d *old_pt;
{
int i;
struct line *p_lines;
struct pt *p_pt,pt_cour;
struct obj **p_temp;
int cx,cy,cz,deb,fin;
struct pt_2d tab_pt[MAX_PT];
/* Calcul du point de depart */
cx=4*p_obj->cx;
cy=4*p_obj->cy;
cz=4*p_obj->cz;
rot(az,&cx,&cy);
rot(ax,&cy,&cz);
rot(ay,&cz,&cx);
/* nouveau angles de rotation */
p_pt=p_obj->p_pt;
ax=((360+ax+p_obj->ax))%360;
ay=((360+ay+p_obj->ay))%360;
az=((360+az+p_obj->az))%360;
/* rotation et passage 3d/2D pour tt les points */
for(i=0;i<p_obj->nb_pt;i++){
pt_cour.x=4*(p_pt->x);
pt_cour.y=4*(p_pt->y);
pt_cour.z=4*(p_pt->z);
rot(az,&pt_cour.x,&pt_cour.y);
rot(ax,&pt_cour.y,&pt_cour.z);
rot(ay,&pt_cour.z,&pt_cour.x);
pt_cour.x+=cx+ox;
pt_cour.y+=cy+oy;
pt_cour.z+=cz+oz;
calc_coord(&pt_cour,&tab_pt[i].x,&tab_pt[i].y);
p_pt++;
}
p_pt=p_obj->p_pt;
p_lines=p_obj->p_lines;
/* affichage des lignes */
for(i=0;i<p_obj->nb_lines;i++){
deb=p_lines->deb;
if(deb>=0){
Move(rp,tab_pt[deb].x,tab_pt[deb].y);
}else{
if(deb==-MAX_PT)deb=0;
Move(rp,old_pt[-deb].x,old_pt[-deb].y);
}
fin=p_lines->fin;
if(fin>=0){
Draw(rp,tab_pt[fin].x,tab_pt[fin].y);
}else{
if(fin==-MAX_PT)fin=0;
Draw(rp,old_pt[-fin].x,old_pt[-fin].y);
}
p_lines++;
}
/***********************************************************/
/* RECURSION: si il y a des elements fils, on les affiches */
/***********************************************************/
if(p_obj->p_tab!=NULL){
p_temp=p_obj->p_tab;
while((*p_temp)!=NULL){
AffObj(rp,*p_temp,ax,ay,az,cx+ox,cy+oy,cz+oz,tab_pt);
p_temp++;
}
}
}
/************** Programme principal ********************************/
main()
{
int i,dir;
struct RasInfo ri;
struct BitMap b1,b2,*b;
struct ViewPort vp;
struct View v,*oldview;
struct RastPort rp1,rp2,*rp;
IntuitionBase = OpenLibrary("intuition.library", 0);
if (IntuitionBase == NULL)
{
printf("intuition is not here. where are we?\n");
goto cleanup1;
}
GfxBase =(struct GfxBase *) OpenLibrary("graphics.library", 0);
oldview=GfxBase->ActiView;
printf ("Initialisation tab cos et sin \n");
for(i=0;i<360;i++){
t_cos[i]=(int)(256.0*cos((float)i*2*PI/360));
t_sin[(i+90)%360]=t_cos[i];
}
InitView(&v);
v.ViewPort=&vp;
InitVPort(&vp);
vp.DWidth=WIDTH;
vp.DHeight=HEIGHT;
vp.RasInfo=&ri;
vp.ColorMap=(struct ColorMap *)GetColorMap(1<<DEPTH);
InitBitMap(&b1,DEPTH,WIDTH,HEIGHT);
InitBitMap(&b2,DEPTH,WIDTH,HEIGHT);
for(i=0;i<DEPTH;i++){
b1.Planes[i]=(PLANEPTR)AllocRaster(WIDTH,HEIGHT);
b2.Planes[i]=(PLANEPTR)AllocRaster(WIDTH,HEIGHT);
}
InitRastPort(&rp1);
InitRastPort(&rp2);
rp1.BitMap=&b1;
rp2.BitMap=&b2;
ri.RxOffset=0;
ri.RyOffset=0;
ri.Next=NULL;
LoadRGB4(&vp,ColorTable,1<<DEPTH);
dir=2;
for(i=0;i<200;i++){
if((i%2)==1){
b=&b1;
rp=&rp1;
}else{
b=&b2;
rp=&rp2;
}
Move(rp,0,0);
ClearScreen(rp);
SetAPen(rp,1);
/* affichage de l'objet */
AffObj(rp,&corp,0,0,0,0,-200,100,NULL);
/* Calcul du mvt des ailes */
corp.ay+=1;
if((i%25)==0)dir=-dir;
aile1.az+=2*dir;
aile_bord.az+=dir;
aile2.az-=2*dir;
aile_bord2.az-=dir;
tete.ay=-aile1.az/2;
ri.BitMap=b;
MakeVPort(&v,&vp);
MrgCop(&v);
LoadView(&v);
WaitTOF();
}
cleanup3:
for(i=0;i<DEPTH;i++){
FreeRaster(b1.Planes[i],WIDTH,HEIGHT);
FreeRaster(b2.Planes[i],WIDTH,HEIGHT);
}
FreeColorMap(vp.ColorMap);
LoadView(oldview);
cleanup1:
if (GfxBase != NULL) CloseLibrary(GfxBase);
if (IntuitionBase != NULL) CloseLibrary(IntuitionBase);
exit(0);
}
|
Mise à jour de mai 2025 : une archive contenant le listing adapté à vbcc, et avec l'exécutable
compilé par vbcc, a été réalisée par Yann-Gaël Guéhéneuc et est disponible sur
obligement.free.fr/files/ant3dcomplexobjects.lha.
|