Suivez-nous sur Mastodon

|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement

|
|
David Brunet

|
|
|
|
Programmation : Assembleur - Routine 3D fil de fer
(Article écrit par Jérôme Étienne et extrait d'Amiga News Tech - mai 1991)
|
|
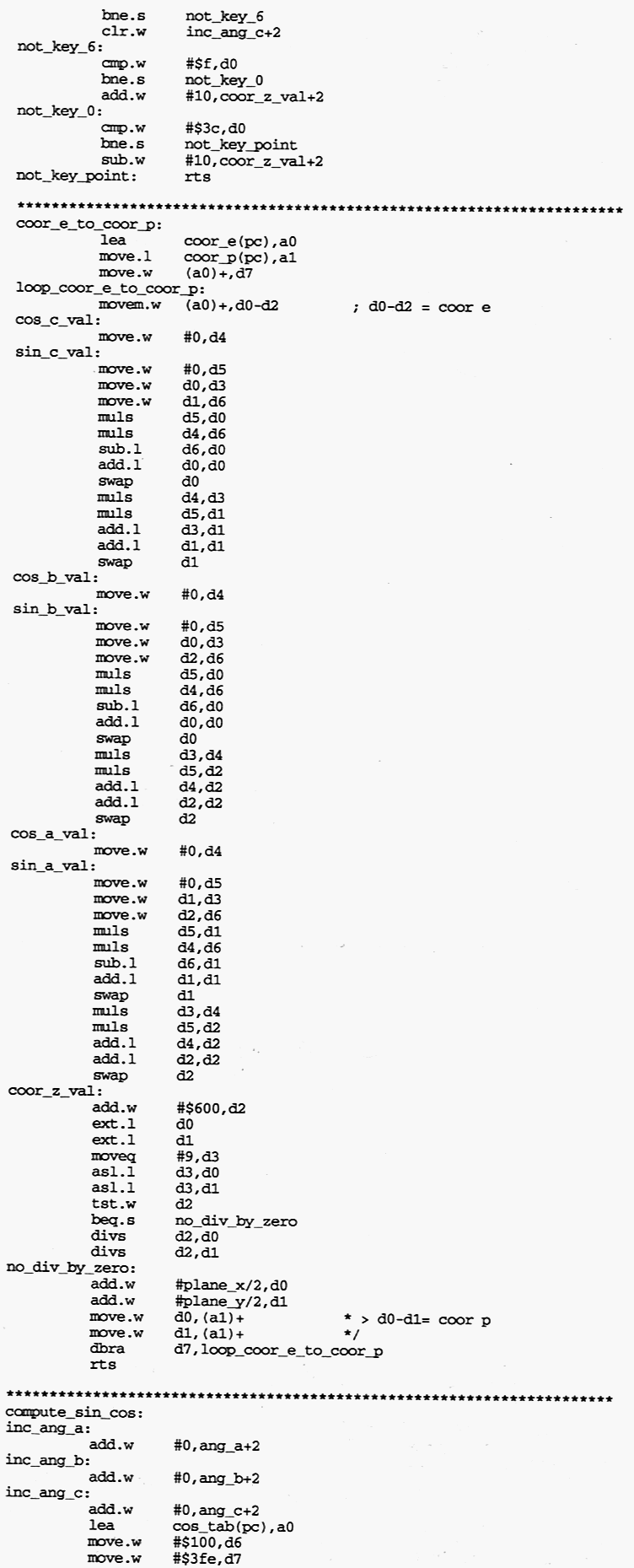
Ce listing est une routine de 3D dite "fil de fer". Cet article se composera de trois parties : la découpe
de droites, les astuces générales et les formules mathématiques.
Il arrive parfois quand on joue avec la 3D ou tout autre programme utilisant des droites, que celles-ci
"sortent" de l'écran, d'où un gros problème : en effet, si l'on n'y prend garde, la droite sera dessinée
dans une zone de la mémoire qui n'a rien à voir avec l'écran, effaçant peut-être une partie du programme
ou de ses données. Il est donc impératif de faire une routine qui gère ce phénomène.
C'est ce que l'on appelle le "clipping" (découpage, en français).
Dans un premier temps, on coupe la droite en y. Pour cela, on fait en sorte que la première
coordonnée (x1, y1) ait le plus faible y. Ainsi, si la seconde coordonnée (x2, y2) est au-dessus
du bord supérieur de l'écran (y_min) ou si la première coordonnée est en dessous de son bord
inférieur (y_max), la ligne est totalement invisible. De plus, si la première coordonnée est
en dessous du bord supérieur et la seconde au-dessus du bord inférieur, la ligne est visible
dans son intégralité (tout du moins en ce qui concerne les y).
Si ces deux tests sont négatifs, alors il existe une intersection de la droite avec les bords.
Si y1<y_min, on calcule l'intersection avec le bord supérieur. De même, si y2>y_max, on calcule
l'intersection avec le bord inférieur.
Il ne reste plus qu'à exécuter les mêmes opérations pour les coordonnées en x. Tout le monde utilise
plus ou moins cette technique, mais on peut ruser sur la manière de calculer les intersections.
Dans le programme, j'utilise la technique dite de "dichotomie". Voici un exemple qui calculera
l'intersection entre une ligne de coordonnées P1(150,20)-P2(400,50) et la droite du bord droit
de l'écran (y=320). 150 est inférieur à 320 et 400 est supérieur à 320 donc l'intersection existe.
On calcule le milieu de la droite xmil=(150+400)/2=275 et ymi1=(20+50)/2=35. On s'aperçoit que
le milieu est à gauche du bord droit, donc on repart en changeant les coordonnées gauches de
la ligne, qui devient donc P1'(275,35)-P2(400,50). On calcule à nouveau le milieu (337,42).
Il est à droite du bord, donc on recommence en installant cette fois-ci les coordonnées droites
de la ligne P1'(275,35)-P2'(337,42). Ainsi de suite, on obtient les coordonnées suivantes :
| Milieu |
Droite |
| (306,38) |
(306,38)-(337,42) |
| (321,40) |
(306,38)-(321,40) |
| (313,39) |
(313,39)-(321,40) |
| (317,40) |
(317,40)-(321,40) |
| (319,40) |
(319,40)-(321,40) |
| (320,40) |
(319,40)-(320,40) |
Enfin, on est parvenu à la droite finale, de coordonnées (150,20x320,40). Dans la réalité,
il faut effectuer cette opération pour chaque bord de l'écran.
Pour connaître les intersections, j'aurais pu aussi utiliser les calculs maniant le coefficient
directeur, c'est-à-dire (y2-y1)/(x2-x1). Il y a dans cette technique une formule pour l'intersection
avec chaque bord. Par exemple, pour le bord droit :
y_inter=y1+(x_max-x1)*(y2-y1)/(x2-x1)
|
Cette formule utilise une multiplication et une division, sans se préoccuper de la taille
de la droite ; elle est donc rapidement plus efficace que la dichotomie. Vous vous demandez peut-être
pourquoi je ne l'utilise pas, si elle est si bien que cela. Ce choix est motivé par les deux
défauts de cette technique : vous vous doutez que le coefficient directeur ne sera pas un nombre
entier, et comme le 68000 ne permet que la division de nombres entiers, nous serons obligés de
simuler une virgule en multipliant par un nombre suffisamment grand avant les calculs, puis de
diviser le résultat par ce même nombre pour obtenir le véritable résultat. Ceci diminue l'erreur
mais ne l'efface pas, ce qui a pour conséquence de donner une impression de tremblement à la
droite en mouvement. De plus réserver, des bits à la partie décimale en enlève à la partie entière.
Voici un exemple où ceci poserait un problème : soit n=6. La partie entière est sur (16-n)=10 bits.
Si celle-ci est supérieure à 2 puissance 10, le résultat ne sera pas du tout celui attendu, donc il
faut faire un test pour détecter ce cas, ainsi qu'une nouvelle routine (Cf. dichotomie) pour calculer
l'intersection dans ce cas. L'aspect de tremblement et un source plus complexe et plus long m'ont
inciter à choisir la dichotomie.
Astuces générales
Vous avez probablement remarqué que je modifie les instructions de "coor_e_to_coor_p"
avec la routine "compute_sin_cos". Cette technique se nomme "l'assembleur automodifié" et permet de
gagner du temps machine et quelques octets (plus précisément, quatre
cycles et deux octets à chaque utilisation des valeurs en question). Donc, on obtient dans
ce cas précis un gain de 4,6 cycles par point calculé.
Autre astuce, l'effacement de l'écran se fait avec le Blitter, qui est quand même l'outil le plus
rapide pour cette opération. Mais la priorité Blitter ne fonctionnant pas dans ce cas, on est
forcé de l'attendre, perdant ainsi beaucoup de cycles inutilement. Au lieu de patienter, on efface
une partie de l'écran avec le 68000, réduisant ainsi la taille du bloc Blitter, et donc le temps nécessaire.
Formules mathématiques
La 3D suppose des calculs relativement complexes, que je ne ferai que citer pour ne pas ennuyer
la galerie. Ils sont programmés dans "coor_e_to_coor_p".
Rotation autour de l'axe (OX) :
Y'=Y*cos(ax)-Z*sin(ax)
Z'=Y*sin(ax)+Z*cos(ax)
|
Rotation autour de l'axe (OY) :
X'=X*cos(ay)-Z*sin(ay)
Z'=X*sin(ay)+Z*cos(ay)
|
Rotation autour de l'axe (OZ) :
X'=X*cos(az)-Y*sin(az)
Y'=X*sin(az)+Y*cos(az)
|
Pour finir, je voudrais signaler que ce source n'as pas pour but de faire la 3D la plus
rapide du monde, mais plutôt d'initier les débutants dans ce domaine. Vous aurez droit le mois
prochain à un source de 3D faces cachées.
Listing 2 : programme GFA Basic pour créer la table des consinus.
|