Suivez-nous sur X
|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement
|
|
David Brunet
|
|
|
|
Programmation : Assembleur - Programmer un défilement sinusoïdal ("sine scroll") sur Amiga (partie 2)
(Article écrit par Yragael et extrait de www.stashofcode.fr - juin 2017)
|
|
Cet article est le deuxième d'une série de cinq consacrés à la programmation d'un "one pixel sine scroll"
sur Amiga, un effet très utilisé par les codeurs de démos et autres cracktros sur Amiga... jusqu'à ce qu'il
soit passé de mode, étant mis à portée de n'importe que minable ("lamer") par le fameux
DemoMaker
du groupe Red Sector Inc., ou RSI :
Le DemoMaker du groupe Red Sector Inc. (RSI), pour minables uniquement
Dans le premier article,
nous avons vu comment installer en environnement de développement sur un Amiga émulé avec WinUAE et programmer
la liste Copper de base pour afficher quelque chose à l'écran.
Dans ce deuxième article, nous allons voir comment préparer une police de caractères 16x16 pour en afficher
facilement les colonnes de pixels des caractères, précalculer les valeurs du sinus requises pour déformer le
texte en modifiant l'ordonnée des colonnes, et mettre en place un triple tampon mémoire pour alterner proprement
les images à l'écran.
Cliquez ici pour télécharger l'archive contenant
le code et les données du programme présenté dans cet article - c'est la même que dans les autres articles.
NB : cet article se lit mieux en écoutant
l'excellent module composé par Nuke/Anarchy
pour la partie magazine de Stolen Data #7, mais c'est affaire de goût personnel...
- Mise à jour du 23/07/2017 : correction d'une erreur mineure dans la figure sur la déformation.
Générer une police 16x16 aux pixels bien ordonnés
A défaut de grives, on se contente de merles. N'ayant pas retrouvé dans nos archives un fichier correspondant
à une police 16x16, nous allons utiliser une police 8x8 dont nous allons doubler les dimensions. Le résultat
ne rendra pas justice à la finesse de l'affichage du défilement sinusoïdal, mais cela permettra de d'avancer.
Le fichier font8.raw contient la police 8x8. Au passage, c'est avec la directive INCBIN qu'on indique à ASM-One
qu'il doit lier le code assemblé avec des données lues dans un fichier :
font8: INCBIN "sources:2017/sinescroll/font8.fnt"
|
C'est une suite des 94 caractères ASCII donnés dans l'ordre, chaque caractère se présentant sous la forme d'une
matrice de 8x8 bits dont les octets sont donnés dans l'ordre - le bitmap du caractère sur un plan de bits.
Visuellement, car l'organisation en mémoire est donc différente, la police se présente ainsi :
Les 94 caractères de la police 8x8, affichés sur plusieurs lignes
Pour produire un "one pixel sine scroll", nous devons dessiner les colonnes de pixels d'un caractère à des
hauteurs variables. Pour dessiner la colonne N, nous n'allons certainement pas perdre du temps à lire la
ligne 0, en extraire la valeur du bit N, dessiner ou effacer le pixel correspondant à l'écran, et répéter
tout cela pour les sept autres lignes. Nous voulons lire en une fois les huit valeurs du bit N formant la
colonne N. Cela impose d'appliquer une rotation de -90 degrés au bitmap :
Transformation de la police 8x8 en vue d'un affichage par colonne
Au passage, comme nous souhaitons disposer d'une police 16x16, nous doublons chaque ligne et chaque colonne :
Agrandissement des caractères
Il en résulte le code suivant, somme toute assez simple :
lea font8,a0
move.l font16,a1
move.w #256-1,d0
_fontLoop:
moveq #7,d1
_fontLineLoop:
clr.w d5
clr.w d3
clr.w d4
_fontColumnLoop:
move.b (a0,d5.w),d2
btst d1,d2
beq _fontPixelEmpty
bset d4,d3
addq.b #1,d4
bset d4,d3
addq.b #1,d4
bra _fontNextPixel
_fontPixelEmpty:
addq.b #2,d4
_fontNextPixel:
addq.b #1,d5
btst #4,d4
beq _fontColumnLoop
move.w d3,(a1)+
move.w d3,(a1)+
dbf d1,_fontLineLoop
lea 8(a0),a0
dbf d0,_fontLoop
|
Dans ce code, la nouvelle police 16x16 est stockée à l'adresse contenue dans "font16". C'est un espace mémoire
de 256*16*2 octets que nous avons alloué plus tôt : 256 caractères de 16 lignes de 16 pixels (deux octets)
chacun, dont le contenu se présente finalement comme une succession de caractères retournés :
La police 16x16 en mémoire (deux octets par ligne)
Faire défiler le texte dans la trame
Après l'initialisation vient la boucle principale. Sa structure est particulièrement simple :
- Attendre que le faisceau d'électrons a atteint - non pas "ait atteint" : ce n'est un pas une éventualité,
c'est une certitude - le bas de la fenêtre d'affichage.
- Dessiner le texte à partir de la position courante et incrémenter cette position.
- Tester si l'utilisateur clique le bouton gauche de la souris, et si non boucler.
Pour attendre le faisceau d'électrons, il suffit de lire sa position verticale sur 9 bits dans VPOSR pour
le bit 8 et VHPOSR pour les bits 0 à 7. Il est important de ne pas se contenter des bits 0 à 7, car affichant
en PAL, nous pourrions décider de spécifier une hauteur de l'écran telle que la position DISPLAY_Y+DISPLAY_DY
dépasse $FF. C'est d'ailleurs bien le cas, puisque $2C+256 donne 300...
Il serait possible d'attendre que le matériel signale la fin de la trame en testant le bit VERTB qu'il
positionne dans INTREQ, puis en effaçant ce bit pour acquitter - le matériel n'efface jamais un bit qu'il
a positionné dans INTREQ :
_loop:
move.w INTREQR(a5),d0
btst #5,d0
bne _loop
move.w #$0020,INTREQ(a5)
|
Toutefois, cela ne surviendrait qu'au dépassement de la ligne 312 - la dernière des 313 lignes du PAL -,
soit bien après la ligne DISPLAY_Y+DISPLAY_DY à partir de laquelle nous n'avons plus rien à dessiner.
Mieux vaut donc attendre que le faisceau d'électron atteigne cette dernière ligne pour enclencher sur le
rendu de la trame suivante. Autant de temps de gagné !
Le code présume que le temps pris par une itération de la boucle principale dépasse celui pris par le
faisceau d'électrons pour tracer les lignes DISPLAY_Y+DISPLAY_DY à 312. Si ce n'était pas le cas, il faudrait
rajouter un test pour attendre le faisceau à la ligne 0. Cela permettrait de ralentir la boucle principale
pour rester calé sur la fréquence d'une trame, c'est-à-dire tous les 50e de seconde en PAL.
Pour tester si l'utilisateur clique le bouton de la souris gauche, il suffit de tester le bit 6 de CIAAPRA,
un registre 8 bits d'un des CIA 8520 qui contrôlent les entrées et les sorties dont l'adresse est $BFE001.
_loop:
_waitVBL:
move.l VPOSR(a5),d0
lsr.l #8,d0
and.w #$01FF,d0
cmp.w #DISPLAY_Y+DISPLAY_DY,d0
blt _waitVBL
;Code à exécuter dans la trame ici
btst #6,$bfe001
bne _loop
|
Ce cadre étant posé, les choses sérieuses peuvent commencer. La première tâche à accomplir en début de trame
consiste à afficher le plan de bits dans lequel nous avons dessiné le défilement sinusoïdal durant la
trame précédente. C'est le principe du double tampon mémoire : ne jamais dessiner dans le plan de bits
affiché pour éviter le scintillement.
Scintillement et double tampon mémoire
Supposons qu'il s'agisse de commencer à dessiner un "R" rouge sur fond vert par-dessus un "Y" bleu sur fond
jaune au moment où le faisceau d'électrons commence à afficher les plans de bits. Il est possible que le
processeur se mette à dessiner le "R" à un moment où le faisceau a déjà affiché une bonne partie du "Y", et
allant plus vite que le faisceau d'électrons, qu'il modifie une partie des plans de bits
que ce dernier n'a pas encore affichée. En conséquence, le faisceau commence à lire les données des plans de bits
après et non avant que le processeur les ait modifiées, et donc à afficher une partie du "R" dans la foulée d'une
partie du "Y" :
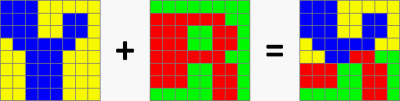Scintillement lors du dessin dans le plan de bits affiché
Quand l'image affichée change à chaque trame, cette course entre le faisceau d'électrons et le processeur
produit un chevauchement d'images successives à partir d'une position qui généralement varie : c'est le scintillement
("flicker").
Pour l'éviter, il faut dessiner le "R" dans des plans de bits cachés, différents de ceux où le "Y" est dessiné,
pour leur part affichés. Quand la trame se termine, il faut demander l'affichage des plans de bits
où le "R" a été dessiné et commencer à dessiner la lettre suivante dans les plans de bits où le "Y" est dessiné.
C'est le double tampon mémoire.
|
Toutefois, nous n'allons pas nous contenter de faire du double tampon mémoire. En effet, comme le Blitter
dispose d'un DMA, il est capable d'effacer un plan de bits tandis que le processeur dessine dans un autre
et que le matériel en affiche un troisième. C'est du triple tampon mémoire :
Permutation circulaire des plans de bits en triple tampon mémoire
Après permutation circulaire des trois plans de bits... :
move.l bitplaneA,d0
move.l bitplaneB,d1
move.l bitplaneC,d2
move.l d1,bitplaneA
move.l d2,bitplaneB
move.l d0,bitplaneC
|
...il suffit donc de modifier l'adresse du plan de bits à afficher là où elle est utilisée pour alimenter
BPL1PTH et BPL1PTL dans la liste Copper :
movea.l copperlist,a0
move.w d1,9*4+2(a0)
move.w d1,10*4+2(a0)
swap d1
move.w d1,11*4+2(a0)
move.w d1,12*4+2(a0)
|
Dès lors, il est possible de lancer l'effacement du plan de bits précédemment affiché au Blitter :
WAITBLIT
move.w #0,BLTDMOD(a5)
move.w #$0000,BLTCON1(a5)
move.w #$0100,BLTCON0(a5)
move.l bitplaneC,BLTDPTH(a5)
move.w #(DISPLAY_DX>>4)!(256<<6),BLTSIZE(a5)
|
Comme cela a été expliqué dans un article précédent, le Blitter peut combiner logiquement bit à bit des
blocs de mémoire sources dans un bloc de mémoire destination. Pour cela, il se base sur une formule qu'il
faut décrire en positionnant des bits dans BLTCON0, une combinaison logique par OR de combinaisons logiques
par AND des données provenant des sources A, B et C, éventuellement inversées par NOT - par exemple,
D=aBc+aBC+ABc+ABC, ce qui revient à D=B, c'est-à-dire à copier dans le bloc de mémoire destination D le
bloc mémoire source B. Si nous spécifions D=0 par omission de tous les autres termes qui peuvent composer
la formule, nous demandons donc au Blitter de remplir de 0 le bloc de mémoire destination.
Le Blitter fonctionnant en parallèle du processeur, nul besoin d'attendre qu'il termine d'effacer l'image
courante de l'animation du défilement sinusoïdal dans son plan de bits pour commencer à dessiner l'image
suivante dans un autre plan de bits. Il sera toujours temps d'attendre le Blitter quand nous voudrons
nous en servir pour dessiner un caractère en lui demandant... de tracer des lignes !
Déformer selon un sinus
Le principe du "one pixel sine scroll" consiste à dessiner les 16 colonnes de pixels qui composent un caractère
à des hauteurs différentes, ces dernières étant calculées en fonction du sinus d'un angle incrémenté entre
deux colonnes.
La formule pour calculer l'ordonnée de la colonne x est donc :
y=SCROLL_Y+(SCROLL_AMPLITUDE>>1)*(1+sin(βx))
|
...où "βx" est la valeur de l'angle β pour la colonne x, incrémenté de SINE_SPEED_PIXEL à
la colonne suivante.
Noter que l'amplitude des ordonnées est alors [-SCROLL_AMPLITUDE>>1, SCROLL_AMPLITUDE>>1], ce qui correspond à une
hauteur de SCROLL_AMPLITUDE+1 si SCROLL_AMPLITUDE est paire et de SCROLL_AMPLITUDE si cette valeur est impaire.
Par exemple, avec SCROLL_Y=0, SCROLL_AMPLITUDE=17 et SINE_SPEED_PIXEL=10 :
Déformation verticale des caractères selon un sinus
Oops ! Nous avons oublié un détail : la fonction sin() ne figure pas dans le jeu des instructions du 68000.
Comme il est hors de question d'appeler une fonction d'une bibliothèque se livrant à des calculs coûteux
en cycles d'horloge du processeur, nous allons précalculer les valeurs du sinus pour tous les angles
de 0 à 359 degrés par pas de 1 degré. Autrement dit, nous allons les tenir à disposition sous la forme
d'une table prête à l'emploi.
Re-oops ! Nous avons oublié un autre détail : nous ne savons pas gérer les nombres à virgule flottante.
Pour les mêmes raisons, nous allons précalculer les valeurs du sinus sous la forme d'entiers. Et comme
l'amplitude des valeurs est [-1, 1], nous allons devoir multiplier ces valeurs par un facteur, sans quoi
elles se limiteraient à -1, 0 et 1. Bref, pour reprendre des formules Excel, nous allons calculer
ARRONDI(K*SIN(A);0), "K" étant le facteur et "A" étant l'angle.
Ce facteur, nous n'allons pas le choisir par hasard. En effet, puisqu'une valeur du sinus sera utilisée
dans une multiplication, l'opération devra être suivie d'une division par le facteur en question. Toujours
dans un souci d'économie, nous excluons de recourir à l'instruction DIVS, très coûteuse en cycles. Ce
sera un décalage arithmétique de bits sur la droite, c'est-à-dire une division entière signée par une
puissance de 2. Le facteur doit donc prendre la forme 2^N.
Nous choisissons de fixer N à 15 pour une excellente précision des valeurs du sinus et la possibilité
d'utiliser une instruction SWAP (décalage de 16 bits sur la droite, donc division par 2^16) suivie
d'une instruction ROL.L d'un bit (décalage d'un bit sur la gauche, donc multiplication par 2), ce
qui sera plus économique en cycles qu'un ASR.L de 15 bits. La table du sinus se présente alors ainsi :
sinus: DC.W 0 ;sin(0)*2^15
DC.W 572 ;sin(1)*2^15
DC.W 1144 ;sin(2)*2^15
DC.W 1715 ;sin(3)*2^15
;...
|
Il reste un petit problème à régler. En effet, effectuer une multiplication signée par 2^N entraîne un
débordement de 16 bits quand la valeur du sinus est -1 ou 1. Ainsi, 1*32768 donne 32768, valeur signée
17 bits qui ne peut donc tenir dans la table des valeurs signées 16 bits du sinus. Dans ces conditions,
cette table ne pourrait pas contenir des valeurs correspondant exactement aux conversions de -1 et 1,
mais seulement très proches approximations : -32767 et 32767.
Nous décidons de ne pas tolérer cette imprécision, et c'est pourquoi N est réduit de 15 à 14, quand bien
même cela nous contraint à faire suivre le SWAP d'un ROL.L de 2 bits au lieu d'un. Démonstration que cela
tient aux limites :
move.w #$7FFF,d0 ;2^15-1=32767
move.w #$C000,d1 ;sin(-90)*2^14
muls d1,d0 ;$E0004000
swap d0 ;$4000E000
rol.l #2,d0 ;$00038001 => $8001=-32767 OK
move.w #$7FFF,d0 ;2^15-1=32767
move.w #$4000,d1 ;sin(90)*2^14
muls d1,d0 ;$1FFFC000
swap d0 ;$C0001FFF
rol.l #2,d0 ;$00007FFF => $7FFF=32767 OK
|
In fine, la table du sinus se présente ainsi :
sinus: DC.W 0 ;sin(0)*2^14
DC.W 286 ;sin(1)*2^14
DC.W 572 ;sin(2)*2^14
DC.W 857 ;sin(3)*2^14
;...
|
Le résultat 16 bits de la multiplication d'une valeur signée 16 bits stockée dans D1 par le sinus d'un
angle exprimé en degrés stocké dans D0 s'obtient ainsi :
lea sinus,a0
lsl.w #1,d0
move.w (a0,d0.w),d2
muls d2,d1
swap d1
rol.l #2,d1
|
Définissons SCROLL_DY comme la hauteur de la bande que le défilement sinusoïdal peut occuper à l'écran.
Partant, SCROLL_AMPLITUDE doit être telle que (SCROLL_AMPLITUDE>>1)*(1+sin(βx)) génère des valeurs
comprises dans [0, SCROLL_DY-16]. Cela n'est possible que si cet intervalle comprend un nombre impair
de valeurs, donc si SCROLL_DY-16 est paire. Cela tombe bien, car nous souhaitons que le défilement
soit centré verticalement à l'ordonnée SCROLL_Y, ce qui impose que SCROLL_DY soit paire, car DISPLAY_DY,
la hauteur de l'écran, est paire. Ce qui donne :
SCROLL_DY=100
SCROLL_AMPLITUDE=SCROLL_DY-16
SCROLL_Y=(DISPLAY_DY-SCROLL_DY)>>1
|
Tant que nous y sommes, nous définissons des constantes définissant l'abscisse à laquelle le défilement
démarre et le nombre de pixels sur lequel il s'étend. Par défaut, ce sera toute la largeur de l'écran :
SCROLL_DX=DISPLAY_DX
SCROLL_X=(DISPLAY_DX-SCROLL_DX)>>1
|
L'ordonnée de chaque colonne d'un caractère du défilement sinusoïdal pouvant être calculée, il est
désormais possible de dessiner ce dernier. Auparavant, il faut mettre en place son défilement et son animation...
|
