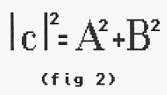Suivez-nous sur X

|
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z,
ALL
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
0,
A,
B,
C,
D,
E,
F,
G,
H,
I,
J,
K,
L,
M,
N,
O,
P,
Q,
R,
S,
T,
U,
V,
W,
X,
Y,
Z
|
|
A propos d'Obligement

|
|
David Brunet

|
|
|
|
Programmation : Assembleur - Ensemble de Mandelbrot
(Article écrit par Emmanuel Hocdet et extrait d'Amiga News Tech - avril 1992)
|
|
Debout les matheux ! Maître Fractale est parmi nous aujourd'hui... Il prendra la forme d'une splendide
Mandelbrot, si prisée des infographistes.
Si vous regardez dans le domaine public, vous trouverez un nombre considérable de traceurs de courbes
fractales, la plupart traitant justement des Mandelbrot. Le problème commun à tous ces programmes est
que l'on n'y comprend absolument rien. De plus, sur un pauvre petit 68000, ça rame, c'est monstrueux !
Je vous propose donc d'étudier le pourquoi du comment mathématique des fractales, ainsi que la réalisation
d'un programme permettant de débusquer la bête (deux fois plus rapidement que
MandelBlitz, le traceur
de Nico François, qui utilise une méthode de calcul plus complexe).
En parlant de complexe, j'espère que vous les maîtrisez... De toute façon, ne vous plaignez pas, je n'aborderai
pas ici la théorie de la dimension fractale, ni sa situation dans un espace topologique en rapport à l'exponentielle
de la matrice carrée du nombre de disquettes rouges de Stéphane modulo le maximum de coups de téléphone
qu'il peut recevoir par jour (croyez-moi, ça fait mal).
Quelques rappels
Un nombre complexe se présente sous la forme d'un couple de nombres : c=A+iB. A et B sont des réels et la
composante i, caractéristique des complexes, est telle que i2=-1. A est dite partie réelle de c et iB,
partie imaginaire.
En fait, le complexe c représente la position d'un point dans un repère (celui de l'écran pour ce qui nous concerne),
avec en abscisse la partie réelle et en ordonnée la partie imaginaire : c désigne donc le point de coordonnées (A,B).
Soient les deux complexes c=A+iB et d=C+iD. On a :
- Addition de deux complexes : c+d=(A+C)+i(B+D)
- Multiplication : c*d=(AC-BD)+i(AD+BC)
- On peut en déduire que : c*c=(A*A-B*B)+i(2AB)
Il faut aussi retenir les formules des figures 1 et 2.
Thé au riz
Nous nous bornerons à l'étude de la formule de cette fractale qui est, il est vrai, l'une des plus simplifiées au
niveau calcul. Nous la devons à un certain Benoit B. Mandelbrot, grand mathématicien d'origine polonaise. Il a
fait ses études en France avant de partir, en 1958, aux États-Unis. La forme quadratique de la formule est représentée
sur la figure 3.
La formule elle-même consiste à répéter n fois cette opération si nécessaire pour un nombre complexe c
quelconque de départ. Soit la suite mathématique de la figure 4.
Nous devons maintenant nous intéresser au comportement de la suite lorsque n tend vers l'infini, c'est-à-dire à
la valeur que prend le module du complexe après n itérations. Il y a deux comportements possibles : soit la valeur
du module grandit de plus en plus vite et tend vers l'infini, soit cette valeur converge, c'est-à-dire qu'elle
se rapproche de plus en plus d'une valeur précise. Ce point fait alors partie de l'ensemble de Mandelbrot.
Mise en oeuvre
Il suffit maintenant de tester chaque point de l'écran pour savoir s'il est, oui ou nom, dans l'ensemble.
Choisissons un repère réel orthogonal, le pixel est considéré alors comme l'unité dans le repère virtuel qu'est
l'écran. Pour les calculs, la distance entre deux points du repère réel correspond à la "distance"
entre deux pixels. Appelons cette valeur "zoom". Plus elle sera petite, plus le Mandelbrot grossira.
Soient (X,Y) les coordonnées d'un pixel à l'écran. Dans le repère réel, ce point a pour coordonnées (x,y) avec
x=x*zoom et y=Y*zoom. Le complexe associé à ce point est c=x+iy. Effectuons alors le calcul
z=c puis z=z+0, z=z+c... Bien sûr, il va bien falloir s'arrêter à un moment. Pour cela, nous avons besoin du
module de z (|z|). Fixons un nombre maximal d'itérations n. Il a été prouvé que lorsque |z| dépasse 2, alors
on est sûr que la suite diverge. Il n'est donc pas nécessaire de continuer le calcul lorsque |z|>2 ou bien,
plus rapide pour les calcul |z|<4. Par contre, si au bout de n itérations |z|<2, le point appartient à l'ensemble
de Mandelbrot ; il suffit alors d'afficher le pixel correspondant d'une couleur caractéristique.
Le programme : le centre de la Mandelbrot se trouve aux coordonnées (0,0) et pour la voir, il faut prendre un
zoom extrêmement petit, de l'ordre du 1/128, pour voir l'ensemble dans sa totalité sur un écran en basse résolution.
Vous imaginez maintenant le problème de lenteur : effectuer des dizaines de multiplications en virgule flottante
par pixel. Vous pouvez vous amuser à programmer le traceur en BASIC, mais le calcul prendra quelques heures...
La ruse consiste ici à effectuer le calcul avec des entiers sur 16 bits (la multiplication 32 par 32 n'existe pas
sur le 68000 et la simuler ferait perdre le temps si durement gagné). Le programme ne travaille qu'avec des nombres
multipliés par 8192, correspondant à un décalage de 13 bits vers la gauche. Après avoir ingurgité toutes ces données,
vous pouvez essayer de faire apparaître, en fonction du nombre d'itérations de chaque pixel, les différentes lignes
de niveau composant la frontière de l'ensemble de Mandelbrot. En portant le calcul sur 32 bits, vous découvrirez,
avec un zoom assez petit, de superbes détails.
Listing 1 : Mandelbrot.s
**** Traceur Mandelbrot par Emmanuel Hocdet pour l'ANT ****
**** A assembler avec devpac 2
D_init=$8200
D_PriB=$400
D_Btpl=$100
D_Copp=$80
D_Blit=$40
D_Spts=$20
Dcon =D_init!D_Copp!D_Btpl
SECTION Mandelbrot,CODE
Start
bsr SaveAll
lea $dff000,a6
move #$7fff,$96(a6)
move.l #copper_list,$80(a6)
clr.w $88(a6)
move #Dcon,$96(a6)
bsr Mandel
bsr RestoreAll
rts
********************************************
SaveAll
move.l 4,a6
jsr -132(a6)
move.w $dff01c,INTENA
or.w #$c000,INTENA
move.w $dff002,DMACON
or.w #$8100,DMACON
rts
RestoreAll
move.w #$7fff,$dff09a
move.w INTENA,$dff09a
move.w #$7fff,$dff096
move.w DMACON,$dff096
move.l 4,a6
lea GFXlib(pc),a1
moveq #0,d0
jsr -552(a6)
move.l d0,a0
move.l 38(a0),$dff080
clr.w $dff088
move.l d0,a1
jsr -414(a6)
jsr -138(a6)
moveq #0,d0
rts
INTENA dc.w 0
DMACON dc.w 0
GFXlib dc.b "graphics.library",0
even
********************************************
Haut=290
Larg=44
taille=Larg*Haut
zoom=64
x1=zoom*Larg*8*3/4
y1=zoom*Haut/2
incy dc.w 0
YY dc.w 0
incx dc.w 0
XX dc.w 0
img dc.w 0 imaginaire de c
real dc.w 0 reel de c
Mandel
lea BITPLAN,a0
move.l a0,d1
lea plans,a1
moveq #0,d0
cree lea 2(a1),a1
swap d1
move d1,(a1)+
lea 2(a1),a1
swap d1
move d1,(a1)+
add.l #taille,d1
dbf d0,cree
move.w #taille/4-1,d0 Efface plan de bits (bitplan)
CLEAR clr.l (a0)+
dbra d0,CLEAR
clr.w YY
clr.w incy
Retour_ligne
clr.w XX
clr.w incx
add #zoom,incy
move incy(pc),d1
sub #y1,d1
move d1,a6 =img
Retour_mot
moveq #15,d4 16 pixels
Retour_pixel
move.w incx(pc),d0 incx
sub #x1,d0
move d0,a5 =real
add #zoom,incx incx
moveq #0,d0
moveq #0,d1
moveq #0,d2
moveq #0,d3
moveq #31,d7 * 32 iterations
FLOOP3
sub.l d3,d2 *****************
lsl.l #3,d2 x=x-y+real
swap d2
add.w a5,d2 *****************
move.w d1,d3 *****************
muls d0,d3
lsl.l #4,d3 y=2*x*y+img
swap d3
add.w a6,d3 *****************
move.w d2,d0 *****************
move.w d3,d1
muls d2,d2 module^2 = x^2+y^2
muls d3,d3
move.l d2,d6
add.l d3,d6 *****************
cmp.l #$10000000,d6 test 4<<(13*2)
dbhi d7,FLOOP3
addq.w #1,d7 si d7=-1 d7+1>0 et le bit X=1
addx d5,d5 donc d5<<1 et recupere le bit X
dbf d4,Retour_pixel
move.w YY(pc),d1
add.w XX(pc),d1
lea BITPLAN,a0 16 pixels a l'ecran
move.w d5,(a0,d1)
btst #10,$dff016
beq.s EXIT
add.w #2,XX
cmp.w #Larg,XX
bmi Retour_mot
add.w #Larg,YY
cmp.w #Larg*Haut,YY
bmi Retour_ligne
EXIT btst #6,$bfe001
bne.s EXIT
rts
SECTION Dans_la_chip,CODE_C
copper_list
plans dc.w $e0,0,$e2,0
dc.l $01001200
dc.l $008e1a71
dc.l $00903dd1
dc.l $00920030
dc.l $009400d8
dc.l $01080000
dc.l $010a0000
dc.l $01800fff
dc.l $01820000
dc.l $fffffffe
BITPLAN ds.b taille
|
Listing 2 : VonKoch_2D.c
/* >&.c.nbbits */
#include <stdio.h>
#include <stdlib.h>
#include <fcntl.h>
#include <math.h>
#define MAXshort 65536
#define Larg_ecr 320
#define Haut_ecr 256
#define X_start 0
#define Y_start Haut_ecr/2-1
#define Larg Larg_ecr
typedef float T_rad ;
typedef float T_coords ;
typedef short Fichier ;
typedef struct _coords {
T_coords X,Y ;
T_rad O ;
} Coords ;
int main ()
{ register i, j, k ;
int divseg, nbrite, nbrnew ;
int NBRsegs=1, Atraiter ;
int f2, TailleSauv ;
T_coords L = Larg ;
T_coords coorX, coorY;
T_rad angleO, totalO ;
T_rad *ptrad, *ptrad_tempo ;
Coords *PtCoords, *PtCoords2 ;
Coords *PtCoords_tempo, *PtCoords2_tempo ;
Fichier *PtSauv, *PtSauv_tempo ;
char *File ;
char name[511] ;
PtCoords=(Coords *)malloc( (NBRsegs+1) * sizeof(Coords) ) ;
PtCoords_tempo = PtCoords ;
PtCoords_tempo->X = X_start ;
PtCoords_tempo->Y = Y_start ;
PtCoords_tempo->O = 0 ;
PtCoords_tempo++ ;
PtCoords_tempo->X = X_start+Larg ;
PtCoords_tempo->Y = Y_start ;
PtCoords_tempo->O = 0 ;
printf ("\n Calcul des coordonnées d'une fractal de Von Koch \n") ;
printf (" Nombre de division du segment : ") ;
scanf ("%d", &divseg) ;
printf (" Nombre de nouveaux segments : ") ;
scanf ("%d", &nbrnew) ;
ptrad = (T_rad *) malloc( nbrnew * sizeof(T_rad) ) ;
ptrad_tempo = ptrad ;
for(i=0; i<nbrnew-1; i++){
printf (" Angle (en deg) du segment %d : ",i+1) ;
scanf ("%f", ptrad_tempo) ;
*ptrad_tempo = *ptrad_tempo * PI / 180 ;
ptrad_tempo++ ;
}
printf ("\n Nombre d'itérations : ") ;
scanf ("%d", &nbrite) ;
for(i=0; (i<nbrite) && (NBRsegs*nbrnew < MAXshort) ; i++){
printf("\nitération %d",i+1) ;
Atraiter = NBRsegs;
L = L / divseg ;
NBRsegs = NBRsegs * nbrnew ;
PtCoords2 = (Coords *) malloc( (NBRsegs+1) * sizeof(Coords) ) ;
PtCoords2_tempo = PtCoords2 ;
PtCoords_tempo = PtCoords ;
for(j=0; j<Atraiter; j++){
coorX = PtCoords_tempo->X ;
coorY = PtCoords_tempo->Y ;
angleO = PtCoords_tempo->O ;
PtCoords_tempo++ ;
totalO = angleO + *ptrad ;
PtCoords2_tempo->X = coorX ;
PtCoords2_tempo->Y = coorY ;
PtCoords2_tempo->O = totalO ;
PtCoords2_tempo++ ;
for(k=0; k<nbrnew-1; k++){
coorX += L * cos(totalO) ;
coorY += L * sin(totalO) ;
totalO = angleO + ptrad[k+1] ;
PtCoords2_tempo->X = coorX ;
PtCoords2_tempo->Y = coorY ;
PtCoords2_tempo->O = totalO ;
PtCoords2_tempo++ ;
}
}
PtCoords2_tempo->X = PtCoords_tempo->X ;
PtCoords2_tempo->Y = PtCoords_tempo->Y ;
PtCoords2_tempo->O = PtCoords_tempo->O ;
free (PtCoords);
PtCoords = PtCoords2;
}
PtCoords_tempo = PtCoords ;
TailleSauv = ((NBRsegs+1)*2 + 1) * sizeof(Fichier) ;
PtSauv = (Fichier *) malloc(TailleSauv) ;
PtSauv_tempo = PtSauv ;
*PtSauv_tempo++ = NBRsegs ;
for(i=0; i<(NBRsegs+1); i++){
*PtSauv_tempo++ = PtCoords_tempo->X ;
*PtSauv_tempo++ = PtCoords_tempo->Y ;
PtCoords_tempo++ ;
/*
printf ("%4d, %4d\n", PtSauv[i*2+1], PtSauv[i*2+2]) ;
*/
}
free (PtCoords) ;
printf ("\n Nom du fichier de sauvegarde : ") ;
scanf ("%s",name) ;
File = (char *) PtSauv;
if ( (f2 = creat(name, 0666)) == -1)
printf ("\n Impossible de créer %s.\n\n",name) ;
else
if ( write(f2, File, TailleSauv) != TailleSauv )
printf ("\n Erreur d'ecriture.\n\n") ;
else printf ("\n Well Done.\n\n") ;
}
|
|